The Physical Universe – Part 6

The quest for unification, continued.

As explored in previous essays in this series, the classical physics laws that govern the large world in which we live (the macro world) are seemingly contrary to the quantum mechanical laws that govern in the world of subatomic particles.  Continuing this essay series on the laws of the physical universe, this essay will explore some of the ways scientists speculate we can bridge those two worlds which, of course, are both part of the same universe.

As Jim Al-Khalili writes in The World According to Physics:

The basic premise of supersymmetric string (or superstring) theory is that one way to unify all the forces is to add more dimensions to space beyond the three we are aware of … [T]he Swedish physicist Oskar Klein suggested that the reason the fifth dimension is hidden is because it is curled up on itself, and therefore too tiny to be detected. There is a standard analogy that helps to explain what this means. From a distance, a hose looks like a one-dimensional line, but zoom in and you see that it is in fact a two-dimensional surface wrapped around into a cylinder. The second spatial dimension (the circular direction around the hose) was too small to be seen from a distance. Klein suggested the same thing applied to Kaluza’s fifth spatial dimension, which was curled up into a circle a billionth of a trillionth of the size of an atom … [I]t did help researchers understand the relevance of the higher dimensions in superstring theory. However, now, instead of just one hidden spatial dimension, there needed to be six, all rolled up into an impossible-to-visualise six-dimensional ball. Superstring theory thus states that there are ten dimensions: four of spacetime that we experience plus the six hidden dimensions. To this day, many researchers looking to unify the forces of nature still work on string theory. They argue that we have come so far, using successful ideas like quantum field theory and supersymmetry to understand three of the four forces; therefore surely gravity can also be tamed. They may well be right. String theory begins with the quantum mechanical properties of matter within spacetime. Its central idea is that all elementary point-like particles are in fact tiny strings, vibrating in the hidden dimensions. These strings would be far smaller than the scales currently probed by particle physics and so we can only experience them as point particles … While the mathematics is elegant and powerful, we still don’t know if string theory [or something else] are the right descriptions of reality.

And there is a rival theory:

This rival theory is just as speculative, but a number of theoretical physicists see it as a purer and more sensible way of tackling unification. It is called loop quantum gravity, and it came to the fore in the last decade of the twentieth century. Loop quantum gravity does not start from quantum field theory, but from the other direction—from general relativity. It assumes that spacetime itself, rather than the matter it contains, is the more fundamental concept. Aesthetically, it would seem sensible to try to quantise the gravitational field—which, according to general relativity, is spacetime itself. Thus, if we shrink down to small enough length scales, we should see space become grainy and discrete. In the same way that Max Planck proposed, in 1900, that heat radiation ultimately comes in quantum lumps, quantizing space suggests there should be a smallest length that cannot be further divided. However, the quanta of gravitational energy are the quanta of space itself, which means that they don’t exist as lumps within space … they are lumps of space. It is thought that the tiniest unit of space—a quantum of volume—is one Planck length, or 10−35 m, across. I have always enjoyed trying to find ways of describing how tiny this volume is. For example, an atomic nucleus contains as many Planck volumes inside it as there are cubic metres in the Milky Way galaxy. This discretisation of space seems inevitable if we want to quantise the gravitational field. And it therefore follows that time must also be ‘lumpy’. So the smooth space and time that we experience is nothing more than a large-scale approximation of the lumpy quanta of gravity, smeared out because the individual pixels of spacetime are too small for us to perceive. Loop quantum gravity contrasts dramatically with string theory, which predicts that, just as the three forces covered by the Standard Model (electromagnetism and the strong and weak nuclear forces) are in fact quantum fields manifested as force-carrying particles, so too is the gravitational field mediated by a quantum particle of gravity: the graviton, a massless state of a string. In string theory, this quantum of the gravitational field exists within spacetime, whereas in loop quantum gravity, it is spacetime itself that is quantised. Loop quantum gravity refers to the closed paths that take you from a quantum of space, via its links to adjacent quanta, around in a loop and back to the starting point. The nature of these loops determines the curvature of spacetime. They are not physical entities like strings. All that is real is the relationship between the loops.

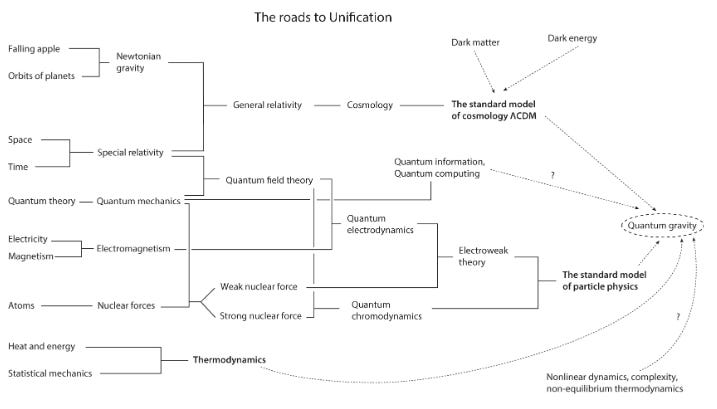
FIGURE. Unification—A (simplified) chart showing how concepts in physics (theories, phenomena, forces) have come together over the years. Note that while the chronology is correct (running from left to right), you should not read too much into it. For example, special relativity appears directly below Newtonian gravity even though it came centuries later.

Don Lincoln, in his Great Courses series The Evidence for Modern Physics: How We Know What We Know, explains in more detail the intriguing possibility that space and time itself are quantized:

We know of four fundamental forces: gravity, electromagnetism, and the strong and weak nuclear forces. At the quantum level, forces like electromagnetism and the strong and weak nuclear forces are best described as a matter particle emitting a force-carrying particle, which is then absorbed by another matter particle. The specifics of the matter particles and force-carrying particles change for the various forces, but it’s the exchange that matters. Gravity is a different thing. The modern theory of gravity is Einstein’s theory of general relativity, where gravity is about the distortion of space. At large size scales, the universe seems to bend and distort under the influence of mass and energy. But we also need to understand how gravity works on the smallest scales. Einstein and others tried to do that without success. Einstein spent the last 30 years of his life trying to unify quantum mechanics and general relativity. He’s known for fighting valiantly against the predictions of quantum mechanics, but it appears that he was wrong—at least in his approach. And he completely ignored the strong and weak nuclear forces. So, how do attempts like the ones Einstein made fail? When quantum mechanics was added to electromagnetism, there were mathematical consequences, including various predictions that had infinities in them. If a physics formula predicts that something should be infinite, it’s probably wrong. But there is a mathematical trick that physicists employ when they calculate quantities using the theory of quantum electromagnetism. It’s called quantum electrodynamics, or QED. Scientists gather up all of the infinities and stuff them together into one location in the equation. They then say those quantities need to be measured in data and put in by hand. In QED, the net result is that there are two of those infinities, and the quantities that need to be measured and put into the equations are the mass of the electron and its charge. This process of hiding away the infinities is called renormalization. Most physicists are not super comfortable with needing to renormalize their calculations, but it works. A quantum theory is called renormalizable if you have a finite number of infinities that you can hide by dumping them into places in the equation where you can replace them by measured quantities. QED has just two such infinities, so physicists are generally happy. But when you try to do the same thing with gravity, things aren’t so neat. Quantum mechanics and gravity combine, and the result is that there is an infinite set of infinities. An infinity is bad, but an infinity of infinities is even worse. This is the reason that nobody has successfully formulated a quantum theory of general relativity. As we learned in the last lesson, it allows us to be able to predict the magnetic properties of the electron to 12 digits of accuracy … To understand why physicists think there must be a quantum nature of gravity, we need to first turn to why they thought that there must be a theory of quantum mechanics governing the orbits of atoms. It was in 1911 that Ernest Rutherford discovered atoms have a nucleus at the center, surrounded by electrons. He didn’t know exactly what the electrons did, but he knew of a paper written by Hantaro Nagaoka that imagined that electrons orbited a small nucleus. There was a problem, though. According to the theory of electromagnetism first worked out in the 1870s by James Clerk Maxwell, any electrical charge will emit radiation when it is accelerated. Any object that moves in a circular path does so because it’s accelerated. Otherwise, it would move in a straight line. y An electron moving in circular orbits has a charge and experiences acceleration. So, it would have to emit radiation, which means it would lose energy. If it lost energy, it would move more slowly, and the electron would eventually spiral down into the nucleus. This would take 16 trillionths of a second. But atoms don’t implode in a fraction of a second, and that’s because of quantum mechanics. In 1913, Niels Bohr proposed the Bohr model of the atom, which says that there is a series of fixed orbits around the atom, each with an increasing unit of spin. The lowest possible orbit has a spin of one unit. So, atomic orbits were proposed to be quantized. According to general relativity, a massive body emits gravitational radiation when it experiences acceleration. And, as we have established, an electron orbiting a nucleus is accelerating. Thus, the same motivation that required the creation of ordinary quantum mechanics also means that there must be a solution of some sort to answer the problems of gravitational radiation in general relativity. That doesn’t mean quantum gravity must be similar to ordinary quantum mechanics. But there are two things that are true. The first is that there needs to be a solution to the problem of the stability of atoms to gravitational radiation. And the second is that general relativity falls apart when it’s applied to the world of the very small. At a minimum, there needs to be a new and improved theory that works in the microcosm. According to currently popular theoretical bias, the smallest possible size is called the Planck length, which is 1.6 × 10−35 meters. The shortest time, called the Planck time, is 5.4 × 10−44 seconds. There is also a Planck energy, a Planck charge, a Planck mass, and a whole bunch of other similar units.

Max Planck was one of the original architects of the first quantum revolution. In 1899, he introduced the Planck constant, which is a unit of electromagnetic action. A unit of electromagnetic action is a constant that relates the frequency of light to the energy of a photon of light with that frequency.

Planck was working on a conundrum of late 19th-century physics. According to the prevailing physics of the time, a glowing object should have been much bluer than was actually observed. But in his paper that accurately predicted the color of hot and glowing objects, he also thought about another issue: how units of measure were arbitrary. He tried to solve this problem in the most scientific way possible. He started with five quantities that any scientifically advanced society can measure: the speed of light, the gravitational constant, the reduced Planck constant, the Boltzmann constant, and the Coulomb constant. Each of those parameters can be measured in any system of units. For instance, the speed of light is about 300,000 kilometers per second or 186,000 miles per second, but either way, the speed of light has units of length divided by time. Planck realized he could take ratios of these five fundamental constants and cancel units, leaving the one unit he wanted. The Planck units were definitely an interesting development, but Planck never imagined that they were anything other than a basis of units. He certainly never imagined that they were, for example, the smallest units of length and time. For that, we have to turn to another researcher. Alden Mead is an American chemist who had an interesting insight about the role of gravity in very small scales. In 1964, he published a paper that considers the effect of gravity on a phenomenon called diffraction, which describes what happens to light when you send it through a small aperture. Because gravity is so incredibly weak compared to electromagnetism, which is the force that governs the behavior of light, its effect is completely ignored in diffraction calculations. But Mead was curious about quantifying gravity’s negligible effect. When you scatter a particle of light off another particle—say, an atom—the atom’s gravitational attraction to the light particle causes an intrinsic uncertainty in the atom’s location. Mead applied Heisenberg’s uncertainty principle to the problem. Heisenberg’s uncertainty principle states that you cannot simultaneously measure the location and motion of a subatomic particle. What he showed is that it’s impossible to determine the position of an object to a precision smaller than the Planck length. His logic can then be extended to short time durations like the Planck time. Mead’s work did not say that the Planck length was the smallest length and the Planck time was the shortest possible time. It said that at those tiny distances and times, the laws of physics as we currently understand them all break down. At the Planck scales, the effect of gravity can no longer be ignored in quantum calculations. [According to Einstein's theory of general relativity, energy and mass curve spacetime. The immense energy densities at the Planck scale result in significant spacetime curvature, meaning gravitational effects become very strong.  There are large energy densities at the Planck scale because, according to the Heisenberg Uncertainty Principle in quantum mechanics, the uncertainty in position and momentum  are related.  At very small lengths, the uncertainty in position is low.  But that means the uncertainty in momentum must be high (because you can’t know both position and momentum).  At very small length scales, such as the Planck length, the uncertainty in momentum (and hence energy, because energy is proportional to the square of the momentum) becomes extremely large. And in quantum mechanics, particles at higher energy levels exhibit greater fluctuations in energy, and high energies cause large effects on spacetime.] It was later that the scientific community began to think that the Planck scale was somehow a smallest scale.  Today, scientists claim that prior to the Planck time, which is 10−43 seconds after the big bang, time didn’t exist. In fact, there are some who claim that time is quantized at these small scales—time was zero, then one Planck time, then two Planck times. In this scenario, there simply isn’t any 1.5 Planck times. Similarly, some researchers claim that space is quantized, coming in discrete chunks of Planck length. If you were super tiny, you could only move in one, two, or three Planck lengths, but never one and a half. But this idea of discrete space and time is really just a theoretical prejudice and not one that we can prove. What we can prove is that at scales like the Planck time, length, and energy, we can no longer ignore gravitational effects. This has to be the size scale where quantum gravity absolutely must become important. It could become important at larger scales, but it’s mandatory at these scales. Furthermore, while it might be possible to look at space at shorter distances, it will require a completely new physical paradigm, with new laws and equations. y So, it’s clear that general relativity breaks in the quantum world. And even if we somehow come up with a better theory of gravity, at the Planck length and time, we have to take quantum effects into account. We don’t know what they will be, but we do know that the future of quantum gravity will be truly fascinating.

Al-Khalili mentions even more areas ripe for future exploration:

[W]e still don’t understand the nature of the dark matter holding galaxies together or the dark energy that is ripping the universe apart; nor do we have answers to fundamental questions like why there is more matter than antimatter; why the properties of the universe are so finely tuned to allow for stars and planets, and life, to exist; whether there is a multiverse; or whether there was anything before the Big Bang that created the universe we see. There is still so much left that we cannot explain. And yet, it is hard not to be dazzled by our success so far.

As Al-Khalili describes, many of those successes so far have led to practical applications that benefit us all:

[Y]ou will be forgiven for thinking that physicists’ obsession with unifying the mathematical principles that govern the workings of nature is all very well—a testament to humankind’s tenacious drive to understand the universe—but so what? Surely, you might think, the discovery of the Higgs boson won’t have any sort of direct impact on our daily lives; nor will the hoped-for theory of quantum gravity help to eradicate poverty and disease. But this is not the right way to look at things. Fundamental, curiosity-driven science has, time and again, led to technological advances that have revolutionised our world … Consider a superficial comparison between physics and engineering. A mechanical or electrical engineering student will study many of the same topics as a physics student, such as Newtonian mechanics, electromagnetism, computing, and the mathematical techniques required for solving certain types of equations that crop up on a regular basis. Indeed, many applied physicists end up working in engineering industries, further blurring the boundaries between the two disciplines. But, typically, a physicist will ask the ‘Why?’ and the ‘How?’ questions in order to expose the underlying principles that govern the workings of nature, whereas an engineer is not normally motivated by these deeper principles and will rather put his or her understanding to work, using it to build a better world. Both physicists and engineers are problem solvers, but they tend to have different motivations for seeking solutions. Just to offer a particular example, the brilliant engineering success of satellite navigation systems (the US GPS being the most important one over the past few decades) clearly demonstrates the value of pure physics research that underpins the engineering. GPS systems are now such an integral part of our lives … [A]n understanding of the quantum rules that explain how electrons behave in semiconductor materials like silicon has laid the foundation of our technological world.  Without an understanding of semiconductors, we would not have developed the transistor and, later, the microship and the computer.  That handheld supercomputer we all carry around with us today (our smartphone) … is packed full of electronic magic, none of which would have been possible without quantum mathematics … Indeed, the entire telecommunications industry relies on technological applications of quantum mechanics, such as lasers and optical amplifiers.  And no modern day hospital could get by without the application of quantum mechanics, from MRI, PET, and CT scanners to laser surgery.

As Al-Khalili writes in another of his books: “In fact, it has been estimated that over one-third of the gross domestic product of the developed world depends on applications that would simply not exist without our understanding of the mechanics of the quantum world.”

Al-Khalili then discusses the fascinating possibilities of quantum computing:

One of the most exciting future applications of physics, without doubt, is the quantum computer.  Such a device would be very different from conventional computers and will be used for a wide range of tasks that are impossible today even with the most powerful supercomputers.  Quantum computers are expected to help humanity solve many of the most difficult problems in science, especially if combined with advances in artificial intelligence.  Quantum computers rely in a very direct way on the more counterintuitive features of the quantum world.  In classical computing, information is stored and processed in the form of ‘bits’ (which stand for binary digits).  A single bit of information can have one of two values: zero or one.  Combinations of electronic switches, each one a physical manifestation of a bit of information that is either on or off, are used to make logic gates, the building blocks that make up a logic circuit.  In contrast, quantum computers operate on what are called quantum bits, or ‘qubits,’ which are not restricted to holding just one or the other of these binary states.  Instead, a qubit can exist in quantum superposition of both zero and one simultaneously, and, as such, can store much more information. The simplest example of a qubit would be an electron whose quantum spin can point either parallel (call this spin ‘up’) or antiparallel (spin ‘down’) to an applied magnetic field.  If an additional electromagnetic pulse is then applied, it can flip the electron’s spin over from parallel (0) to antiparallel (1).  But because an electron is a quantum particle, the electromagnetic pulse can also put it in a superposition of spin up (0) and down (1) at the same time.  Two entangled electrons can be put into a superposition of four possible quantum states – 00, 01, 10, and 11 – simultaneously.  With many more qubits, complicated quantum logic circuits can be developed.  When multiple qubits are entangled together, they can act coherently and therefore process multiple options simultaneously, which makes them far more powerful and efficient than their classical counterparts.  But there are problems with realizing such a device.  Quantum entangled states are extremely delicate and can only be maintained under special conditions for short periods of time.  The challenge is not only to isolate and protect these states from their surrounding environment, which destroys quantum coherence, but to be able to control the input and output of the information that the qubits process.  And this gets progressively more difficult the larger the number of entangled qubits. The beauty of quantum computers is that their processing speed scales exponentially with the number of qubits.  Consider the information content of three non-quantum switches.  Each can be either 0 or 1, and so there are eight different combinations: 000, 001, 010, 100, 011, 101, 110, 111.  But three entangled qubits allow us to store all eight combinations at once.  Each of the three digits is both a 1 and a 0 at the same time.  On a classical computer, the amount of information increases exponentially with the number of bits.  So N bits means 2-to-the-N different states.  A quantum computer with N qubits can make use of all 2-to-the-N states at once … A number of theoretical physicists are pinning their hopes on quantum computing to help them out.  This is because a quantum computer by its very nature should be in a position to accurately simulate the quantum world and maybe even help them find the right theory of quantum gravity.

That concludes this essay series on the physical universe.

Links to other essays in this series: Part 1; Part 2; Part 3; Part 4; Part 5; Part 6.