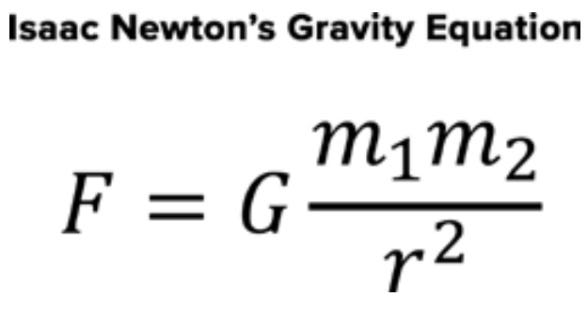The Physical Universe – Part 5

The quest for unification.

Continuing our exploration of our understanding of modern physics, in this essay we’ll examine recent efforts to further “unify” physics by subsuming its laws under even more general rules, refining our understanding of the inter-connectedness of everything as we learn more and more.

Sean Carroll gives an excellent summary of our earlier progress toward a unified theory in the second lecture of his Great Courses series on The Many Hidden Worlds of Quantum Mechanics.  As Carroll writes:

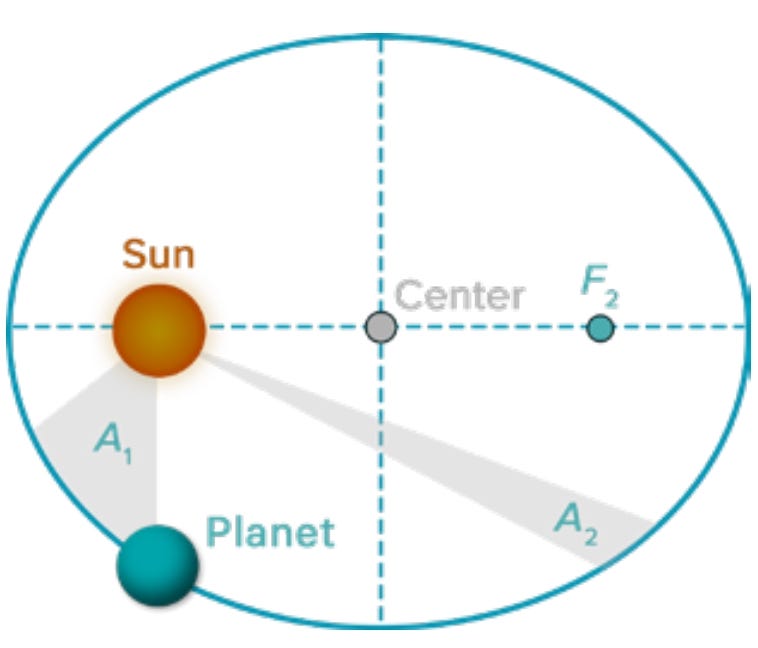
The history of physics can be divided into three eras. The first era can be traced to Aristotle, a Greek philosopher who lived in the 4th century BC. The second era belongs to classical physics, which was codified by Newton in the 17th century. That lasted until the quantum revolution of the 20th century … [T]o understand classical physics, at least a nod should be given to Aristotle. In Aristotle’s view, you can think of objects as having a natural state of being, which is typically at rest wherever they want to be. To get something moving, in Aristotle’s view, you have to exert a force on it. When the force ceases, the object will stop moving. Although this is very different than the physics that came later, it’s compatible with what you see in the world. A coffee cup on a table will just sit there unless you push it. And when you stop pushing it, it will stop moving. Today, that behavior is attributed to friction from the table. Aristotle’s way of thinking was that it was just the natural thing the coffee cup wanted to do. So, a big change from Aristotle to classical mechanics is that things tend to keep moving as long as you don’t stop them. That’s called conservation of energy and momentum in classical mechanics. Many thinkers contributed to this idea, but Newton developed it into a full-blown framework. To do that, he needed both precise definitions of important concepts and equations relating them to each other. A major impetus for the development of classical mechanics came from astronomy, especially the motions of the planets in the solar system. Nicolaus Copernicus famously suggested that the earth and all the other planets move around the sun, rather than the sun and the planets moving around the earth. That was a good idea, but in order to fit the observations that people had collected over the years, Copernicus needed to invoke a complicated set of interlocking circles to describe the orbits. German astronomer Johannes Kepler realized everything would be much simpler if the planets moved in ellipses rather than in circles and developed a set of simple laws of planetary motion, according to which planets move faster when they’re closer to the sun. But he didn’t explain why this would be the case. Meanwhile, other scientists were developing ideas like force and acceleration. In the late 1600s, members of the new Royal Society in England talked about how to derive the orbits of the planets rather than merely postulating them. Robert Hooke suggested that there was a force stretching from the sun to the planets that diminished with distance as 1 over the distance squared, a famous inverse square law: F = 1/d(squared).

He suggested that such behavior would naturally lead to elliptical orbits, but he didn’t quite have the mathematical chops to be able to prove that. Eventually, Hooke and Christopher Wren (a famous architect and the designer of Saint Paul’s Cathedral) convinced their friend Edmond Halley (who would eventually become famous for discovering the comet) to make the journey from London to Cambridge, home of Newton, to ask him about this problem. Newton replied that he’d already calculated that an inverse square law would naturally give rise to elliptical orbits, and Halley encouraged him to publish his calculation. This grew into Newton’s masterwork, Philosophiae naturalis principia mathematica, which was published in 1687. In this book, Newton not only established his law of universal gravitation, a version of the inverse square law, but he also presented the general laws of motion that formed the basis of classical mechanics as well as the first glimmers of the mathematical techniques of calculus.

Classical mechanics is radically different from the Aristotelian perspective. Objects naturally remain in motion at a constant velocity unless they are acted on by an outside force. The basic idea of classical mechanics is that every system—such as a planet or anything else moving according to the classical laws of motion—has a state, and that state consists of its position and its velocity. There is also a net force acting on the system. The force could be zero, but it has a number. In fact, it’s a vector, so it has a magnitude and a direction. And then there is a crucial rule that relates the acceleration to the force— namely, Newton’s second law of motion, F = ma, or force equals mass times acceleration. This says that if the force is zero, the acceleration is zero. That means that the object will keep moving at a constant velocity. And if the force is not zero, the velocity will change due to the acceleration. So, the force on an object is simply determined by its environment— meaning all the other stuff in the universe. So, to get classical mechanics off the ground, you don’t need to separately specify the force acting on an object. In principle, the forces acting on an object are fixed by the rest of the universe. That has a profound implication. If you’re given the state—the position and the velocity of everything in the universe—then what happens at the next moment will be entirely fixed by the laws of physics. Then, you can use calculus—the mathematical technique that Newton, as well as his contemporary Gottfried Wilhelm Leibnitz, developed—to chug forward in time, determining the entire trajectory of the object based on that initial state. So, classical mechanics is deterministic: Both the future and the past are fixed by events at any one moment.

This idea took a while to sink in. Newton didn’t really emphasize it. Around the year 1800, French mathematician and scientist Pierre-Simone Laplace pointed out that, if you knew the position and velocity of everything in the universe and you had infinite calculational powers, both the past and future would in principle be known to you, according to the principles of classical mechanics. This hypothetical being that Laplace suggested—someone who knew everything and could do any calculation—is now known as Laplace’s demon. It’s important to recognize that it’s a thought experiment: There is no prospect of ever having such information, even in the future, when computations get very good. It’s meant as an illustration of the power of classical physics— that in principle everything is determined from what is going on at any one moment in time. And any system using this basic framework is called classical. That includes the theory of relativity that will come along early in the 20th century.

A paradigmatic example of a classical theory is Newton’s theory of gravity, which says that the force of gravity between two objects is proportional to the mass of each object and to the inverse of the distance between them squared. That’s the inverse square law. Using this as a starting point—using F = ma, this classical mechanics equation, and his law of universal gravitation—Newton was able to rederive all of Kepler’s laws of planetary motion. He also moved beyond those laws to think about how the gravitational field of each planet would perturb the motions of the other. In other words, it’s not just the sun’s gravitational field that matters. All the planets are constantly exerting a slight gravitational pull on the other planets, and that disturbs them from moving in perfect ellipses as Kepler would have suggested. This kind of thinking eventually led to the discovery of the planet Neptune, which was proposed to explain the anomalous motion of Uranus and the other outer planets.

But Newton’s gravitational law leads to a philosophical puzzle: How does a planet know what the gravitational pull exerted by the sun is supposed to be? What is the medium that carries the force from the sun to the planets? Without knowing what that is, it would seem like what’s being proposed is action at a distance. The sun is in one place, and somehow the planets know how far away the sun is—what the gravitational force is supposed to be. Action at a distance is something that physicists generally disapprove of. Newton knew this and wrote about it in the Principia, and he decided to leave the problem to future generations. There is a resolution to this, at least in classical mechanics. The resolution was suggested by Laplace, who said that rather than thinking directly of one object exerting a force on another—the sun and a planet exerting a gravitational force on each other—instead imagine there is a field pervading space. A field is a mathematical entity that exists everywhere throughout space. Rather than having a specific location like a particle, the field has a value at every point. An example of a field that you’re familiar with is the air temperature on the ground at different points around the globe. So, the idea of fields was introduced by Laplace, but it didn’t matter much. The same predictions resulted from both Laplace’s version of gravity and Newton’s. In the 19th century, it became a much more important idea, because that saw the advent of electromagnetism. At every point in space, both the electric and the magnetic fields have a magnitude and a direction in which they point. So, the values of these fields are vectors. The way that electromagnetism works is that charges at rest create an electric field. A charge in motion generates a magnetic field. This notion was developed by Michael Faraday and turned into a rigorous mathematical system by James Clerk Maxwell—who unified electricity and magnetism into the single theory of electromagnetism.

Maxwell’s electromagnetism also explained what light is: a wave in the electromagnetic field. That’s an early triumph of the idea of unification in physics: Electrical and magnetic forces are unified with light. These theories—the theories of gravity and of electromagnetism—refer to fields rather than particles, but they’re still part of classical mechanics. Rather than the position of a particle, you just use the value of the field at each point. Electromagnetism plays a big role historically, not just because electromagnetism is intrinsically important, but with its special role for the speed of light, electromagnetism was the inspiration for the next big revolution in physics: the theory of relativity.

In Maxwell’s theory, electric and magnetic fields are two aspects of a single underlying phenomenon. It’s just being looked at in different reference frames, or different states of motion. But what’s a state of motion? Who decides what’s moving and what’s not? Long ago, Galileo pointed out that there is no preferred state of rest in classical mechanics. Instead, there are relative velocities. If you have two objects, you can ask what the velocity of the objects relative to each other are, but you can’t say that there’s an absolute velocity for either one of them. This is called Galilean relativity, and it’s part of Newtonian mechanics. When electromagnetism came along, it seemed to require something new—a medium through which these electromagnetic waves could move. If light is supposed to be a wave of electromagnetism, what is waving? The answer was given the name the luminiferous ether. But although experimentalists looked for this ether, they found no evidence that it existed. In 1905, Albert Einstein said that there was no ether and instead postulated that the speed of light is an absolute quantity. It’s measured to be the same by every observer, no matter how that observer is moving through the universe. This requires a radical rethinking of what is meant by distance in space as well as time. This rethinking is now known as special relativity.

Einstein’s professor Hermann Minkowski pointed out that the simplest way of thinking about Einstein’s theory is to combine space and time together into a new thing called space-time—another example of unification in physics—which was adopted eventually by Einstein. And in 1915, 10 years after formulating special relativity, Einstein proposed that space-time, a field, can be warped and bent, and that bending and warping is perceived as the force of gravity. This is now called the theory of general relativity, as opposed to special relativity, which is about the speed of light being constant.

The forces of nature, such as the electromagnetic force and the gravitational force, are being mediated by fields. So, fields play a crucial role in the fundamental architecture of physics. Meanwhile, physicists were drawn to think about matter as consisting of atoms—or, more generally, particles. In the early 1800s, chemist John Dalton realized that there were two possible compounds you could make out of tin and oxygen: a white powder and a black powder. He figured out that if you had a fixed amount of tin, it took exactly twice as much oxygen to make one of these compounds as the other. This fact—exactly twice as much—is hard to explain if tin and oxygen are continuous, smoothly varying quantities. But it’s easy to explain if they’re made of discrete atoms: One powder has a single oxygen atom, while the other has two oxygen atoms in it. The word atom comes from the ancient Greek word for “indivisible.” But that turned out not to be quite accurate. In 1897, J. J. Thompson discovered particles called electrons, which are much smaller than even the lightest atoms (hydrogen atoms). Electrons have a negative electric charge, whereas a typical atom has zero charge. Eventually, Ernest Rutherford put together the well-known picture of an atom, which looks like a solar system. There is a massive, compact nucleus at the center of the atom with much later electrons orbiting around it.

Today, it is known that the nucleus is made of some combination of positively charged particles called protons and electrically neutral particles called neutrons. And protons and neutrons are both made of even smaller particles called quarks. So, matter seems to be made of particles. Every atom in the periodic table is some combination of three kinds of particles: protons, neutrons, and electrons. And if you put yourself in the mindset of a physicist as the 19th century turned into the 20th, you might have thought that you were close to the ultimate theory of all of physics. But as it turns out, a radical rethinking was indeed in the cards, in the form of quantum mechanics.

That quest for unification continues in the quantum age.  Again, we’ll turn to Jim Al-Khalili’s The World According to Physics.  Al-Khalili writes that physicists have a “relentless drive to unify their theories—to bring together the laws of the universe and encapsulate them in a single neat mathematical equation—a ‘theory of everything’.”  He continues:

Throughout the history of physics, the more we’ve discovered about the workings of nature, the more connections we’ve found between seemingly unconnected forces and particles, and the fewer rules and principles we’ve needed to explain an ever-wider range of phenomena. Unification is not something we deliberately set out to achieve; it has emerged as a result of our deeper understanding of the physical world. Physicists have so far had a good deal of success with this broad project of unification … Newton understood that what causes the apple to fall from the tree is the same universal force (gravity) that controls the motion of the heavenly bodies across the sky. This was not at all obvious at the time, even though it might seem so to us today. Before Newton, it was believed that objects fell to the ground because everything had a ‘tendency’ to move to its ‘natural’ place—towards the centre of the world—and that the motion of the Sun, Moon, planets, and stars was subject to very different principles. Newton’s law of universal gravitation brings these phenomena together by stating that all masses are attracted towards each other, with a force proportional to the product of their mass and inversely proportional to the square of the distance between them. It doesn’t matter whether it is an apple or the Moon; the same formula governs the way both are attracted by the Earth. Another huge leap forward along the path to unification took place almost two centuries after Newton, when James Clerk Maxwell showed that electricity and magnetism are in fact different facets of the same electromagnetic force. So, the electrostatic attraction between a scrap of paper and a balloon that has been rubbed on your clothing has its origin in the same electromagnetic force that attracts a paper clip towards a magnet. Almost all phenomena we see in nature are due ultimately to one or other of these two forces: gravity and electromagnetism. It was therefore natural to ask whether we can go further and bring them together in a combined theory … [A]t a fundamental level, the gravitational field is nothing more than the shape of spacetime itself, a revelation that was also due to a unifying idea. By combining space with time, Einstein revealed a profound truth: that only in four-dimensional spacetime can all observers (however fast they are moving relative to each other) agree on the separation between two events. A decade later, his general theory of relativity gave the world a new and more accurate picture of how mass and energy cause this spacetime to curve. But that wasn’t enough for Einstein, who spent the most part of the next four decades of his life searching unsuccessfully for a unified theory that would combine his theory of gravity with Maxwell’s electromagnetic theory. We now know that there are, in addition to gravity and electromagnetism, two other forces—the strong and weak nuclear forces—that only act over very tiny distances, but which are just as important as far as the fundamental laws of nature are concerned. And it was the unification of the electromagnetic force with one of these nuclear forces that would be the next step forward in twentieth-century physics. But this important advance in our understanding of the nature of the fundamental forces only came about with the evolution of quantum mechanics from a theory describing the microcosm in terms of particles and waves to one involving fields … [Q]uantum field theory describes how electrons emit and absorb photons, and how two electrons will repel each other, not by some invisible force that links them across space, but by the exchange of photons.  [To be clear, in the framework of quantum electrodynamics (QED), the electromagnetic force is mediated by the exchange of virtual photons, which cannot be observed but whose effects can be observed. Mathematicians use the term “virtual photon” to describe whatever it is that is producing that effect.  Electrons interact by exchanging these virtual photons, resulting in the repulsive electromagnetic force. This can be visualized as electrons emitting and absorbing virtual photons, which imparts momentum and causes the electrons to repel each other.]  By the 1930s, the distinction, at the quantum level, between the physics of particles and the physics of fields was swept away. So, in the same way that photons are the particle-like manifestations of the electromagnetic field—lumps of pure energy at the quantum scale—so too are the localised particles of matter, such as electrons and quarks, just manifestations of their more fundamental associated quantum fields. However, unlike photons and the electromagnetic field, this is not so obvious when it comes to the matter particles. The reason for this is that photons can bunch together in unlimited numbers, giving rise to what we perceive as an electromagnetic field on the macroscale, whereas matter particles like electrons and quarks are less sociable, thanks to one of the rules of quantum mechanics called the Pauli exclusion principle, which states that no two identical matter particles can occupy the same quantum state. This means we do not perceive their quantum fields so easily. By the late 1940s, mathematical problems with the description of quantum fields were finally resolved, and the theory known as quantum electrodynamics (QED) was completed. To this day, it is regarded as the most accurate theory in all of science. It is also the physical theory that explains at a fundamental level almost everything in the world around us, since it underpins all of chemistry and the nature of matter—from the way the electronic circuitry and microchips in my laptop work to the neurons firing in my brain, commanding my fingers to move across the keyboard. This is because QED is at the heart of all interactions between atoms. And yet, for all its power, QED still describes only one of the four forces of nature: electromagnetism. During the late 1950s and ’60s, physicists used beautiful but complicated mathematical reasoning to combine QED with a field theory of the weak nuclear force. They showed that the weak force was, at a fundamental level, also generated by exchanged particles equivalent to the role played by exchanged photons in describing the electromagnetic force. Today, we have a unified theory describing a single ‘electroweak’ interaction that, through a process called symmetry breaking, splits into two distinct physical forces: electromagnetism (manifested by the exchange of photons) and the weak force, carried by the exchange of the W and Z bosons … [A]nother quantum field theory was developed to describe the strong nuclear force that holds the quarks together inside protons and neutrons. A subtlety of the strong force is that the way it acts between quarks involves a property called ‘colour charge’, which deserves a brief mention. Just as particles that feel the electromagnetic force come in two types of electric charge, which we refer to simply as positive and negative,1 the particles that feel the strong force (quarks) come in three types of ‘charge’, named colour charge to distinguish them from electric charge. Note that the word ‘colour’ here is not to be taken in any way literally. The reason three types of colour charge were needed, rather than just two (as with electric charge), was to explain why protons and neutrons must each contain three quarks; and the reason the analogy with colour was chosen was because of the connection with the way the three different colours of light (red, blue and green) combine to produce white light. Thus, the three quarks in a proton or a neutron each carry a different colour charge: red, blue or green, which combine to produce a particle that has to be ‘colourless’. The rule was that quarks could not exist by themselves because they carried colour; they could only exist in nature by sticking together to make up colourless combinations. For this reason, the field theory of the strong nuclear force that binds quarks together became known as quantum chromodynamics, or QCD. The exchange particles between quarks are the gluons, a rather more evocative and appropriate name, I think you’ll agree, than that of those weak force–carrier particles, the W and Z bosons.

As Al-Khalili summarizes the current state of science:

So, this is where we are at the moment: stuck with two successful frameworks—quantum field theory and general relativity—which just don’t seem to want to fit together. Indeed, they appear to have very little in common: their mathematical structures are incompatible. And yet this cannot be the whole story. We know that spacetime reacts to the matter within it. We also know that matter at the subatomic scale behaves according to the rules of quantum mechanics, which must surely in turn affect the behaviour of spacetime. If an unobserved electron is in a quantum superposition of being in two or more states at once, as we know electrons can be—for example, if their quantum state is spread out over some volume of space or in a superposition of different energies at once—then surely the spacetime around this electron must reflect this fuzziness too. The problem is that general relativity just isn’t ‘quantum-y’, and it is far from straightforward how we can make it so. One of the problems with this is that subatomic particles have such tiny masses that their effect on spacetime is nigh impossible to measure. Still, the issue remains: How do we quantise the gravitational field? What do we need to do to bring quantum field theory and general relativity together?

Those are questions we’ll explore in the next essay in this series.

Links to other essays in this series: Part 1; Part 2; Part 3; Part 4; Part 5; Part 6.