The Physical Universe – Part 4

Quantum mechanics.

Continuing our essay series on the basic laws of physics, this essay draws again from Jim Al-Khalili’s book The World According to Physics.

Al-Khalili describes that, at very small scales even below the scales of atoms, yet another, much different physics is at work, namely quantum mechanics:

Quantum mechanics is seen, quite rightly, as the most fascinating, yet at the same time most mind-boggling and frustrating scientific theory ever devised by humankind … "[Q]uantum mechanics as the most powerful and important theory in all of science. After all, it is the foundation on which much of physics and chemistry is built, and it has revolutionised our understanding of how the world is built from the tiniest of building blocks … The first major theoretical breakthrough—the concept of the ‘quantum’—was made by the German physicist Max Planck. In a lecture in December 1900, he proposed the revolutionary idea that the heat energy radiated by a warm body is linked to the frequency at which its atoms vibrated, and consequently that this radiated heat is ‘lumpy’ rather than continuous, emitted as discrete packets of energy, which became known as quanta. Within a few years, Einstein had proposed that it wasn’t just Planck’s radiation that was emitted in lumps, but that all electromagnetic radiation, including light, came in discrete quanta. We now refer to a single quantum of light—a particle of light energy—as a photon … Particles of matter, such as electrons, can exhibit a wavelike nature, too. This general notion, tested and confirmed for almost a century now, is known as wave-particle duality and is one of the central ideas of quantum mechanics. This does not mean that an electron is both a particle and a wave at the same time—but rather that, if we set up an experiment to test the particle-like nature of electrons, we find that they do indeed behave like particles. But if we then set up another experiment to test if electrons have wavelike properties (such as diffraction or refraction or wave interference), we see them behaving like waves. It’s just that we cannot carry out an experiment that would show both the wave and particle nature of electrons at the same time.

The odd phenomenon that both the wave nature and the particle nature of matter cannot be measured at the same time has resulted in a situation in which the location and speed of a subatomic particle can only be predicted in terms of probability.  The problem of measurement in quantum mechanics is closely tied to the probabilistic nature of quantum systems. A quantum system exists in a “superposition” of possible states until it is measured, at which point it “collapses” into one of its possible states with certain probabilities. This probabilistic behavior arises from the inherent uncertainty and indeterminacy of quantum mechanics.  The Heisenberg Uncertainty Principle is a fundamental concept that describes the inherent limitations in simultaneously knowing the precise position and momentum of a particle. Formulated by Werner Heisenberg, the principle highlights that the more precisely we know a particle's position, the less precisely we can know its momentum, and vice versa. This intrinsic uncertainty is not due to measurement limitations but is a fundamental property of nature at the quantum level:

This balance between how much we can simultaneously know about an electron’s particle nature (its position in space) and its wave nature (how fast it is travelling) is governed by Heisenberg’s uncertainty principle, which is regarded as one of the most important ideas in the whole of science and a foundation stone of quantum mechanics. The uncertainty principle puts a limit on what we can measure and observe, but many people, even physicists, are prone to misunderstanding what this means. Despite what you will find in physics textbooks, the formalism of quantum mechanics does not state that an electron cannot have a definite position and a definite speed at the same time, only that we cannot know both quantities at the same time. A related common misunderstanding is that humans must play some kind of crucial role in quantum mechanics: that our consciousness can influence the quantum world, or even bring it into existence when we measure it. This is nonsense. Our universe, all the way down to its elementary building blocks at the quantum scale, existed long before life began on Earth—it wasn’t sitting in some fuzzy limbo state waiting for us to come along, measure it, and make it real. By the mid-1920s, physicists were beginning to realise that the concept of quantisation is more general than just the ‘lumpiness’ of light or the ‘waviness’ of matter. Many physical properties, familiar to us as continuous, are, in fact, discrete (digital rather than analog) once you zoom down to the subatomic scale. For example, the electrons bound within atoms are ‘quantised’ in the sense that they can only have certain specific energies and never energies in between these discrete values. Without this property, electrons would continuously leak energy while orbiting the nucleus, meaning that atoms would not be stable and complex matter, including life, could not exist. According to nineteenth-century (pre-quantum) electromagnetic theory, negatively charged electrons should spiral inwards towards the atom’s positively charged nucleus. But their quantised energy states prevents this from happening. Certain quantum rules also define which energy states the electrons occupy and how they arrange themselves within atoms. As such, the rules of quantum mechanics dictate how atoms can bind together to make molecules, making quantum mechanics the foundation of the whole of chemistry. Electrons are able to jump between energy states by emitting or absorbing the correct amount of energy. They can drop to a lower state by emitting a quantum of electromagnetic energy (a photon) of exactly the same value as the difference in energies between the two states involved. Likewise, they can jump to a higher state by absorbing a photon of the appropriate energy. The sub-microscopic world, down at the scale of atoms and smaller, therefore behaves very differently from our familiar everyday world. When we describe the dynamics of something like a pendulum or tennis ball, or a bicycle or a planet, we are dealing with systems comprising many trillions of atoms, which are far removed from the fuzziness of the quantum realm. This allows us to study the way these objects behave using classical mechanics and Newton’s equations of motion, the solutions of which are an object’s precise location, energy or state of motion, all knowable simultaneously at any given moment in time … Typically, we would solve Schrödinger’s equation to calculate a quantity called the wave function, which describes not the way an individual particle move along definite path, but the way its ‘quantum state’ evolves in time. [The wave function contains all the information about the system and can be used to calculate probabilities.] The wave function can describe the state of a single particle or group of particles and has a value that provides us with the probability of, say, finding an electron with any given set of properties or location in space if we were to measure that property. The fact that the wave function has value at more than one point in space is often wrongly taken to mean that the electron itself is physically smeared out across space when we are not measuring it. But quantum mechanics does not tell us what the electron is doing when we are not looking—only what we should expect to see when we do look … Despite its tremendous success, if we dig a little deeper into what quantum mechanics tells us about the microcosm, we could easily lose our minds. We ask ourselves, ‘But how can it be so? What am I not ‘getting’?’ The truth is, no one really knows for sure. We do not even know if there is any more to ‘get’. Physicists have tended to use terms like ‘strange’, ‘weird’, or ‘counterintuitive’ to describe the quantum world. For, despite the theory being powerfully accurate and mathematically logical, its numbers, symbols and predictive power are a facade hiding a reality we find difficult to reconcile with our mundane, commonsense view of the everyday world. There is, however, a way out of this predicament. Since quantum mechanics describes the subatomic world so remarkably well, and since it is built on such a complete and powerful mathematical framework, it turns out we can manage just fine by learning how to use its rules in order to make predictions about the world and to harness it to develop technologies that rely on those rules, leaving the hand-wringing and head-shaking to the philosophers.

Sean Corroll, a wonderful science explainer from John Hopkins University, explores more of the “deep meaning” aspects of quantum physics in his Great Courses lecture series The Many Hidden Worlds of Quantum Mechanics:

Discussions about the foundations of quantum mechanics often center on the measurement problem. But another important issue is the reality problem: Does the wave function represent reality, or is it merely a useful way of making predictions for observations? In the Copenhagen interpretation [the interpretation given by scientists Niels Bohr, Werner Heisenberg, and Max Born], the wave function does not represent reality. But there are other formulations of quantum mechanics—many-worlds being one of them—where the wave function does represent reality.

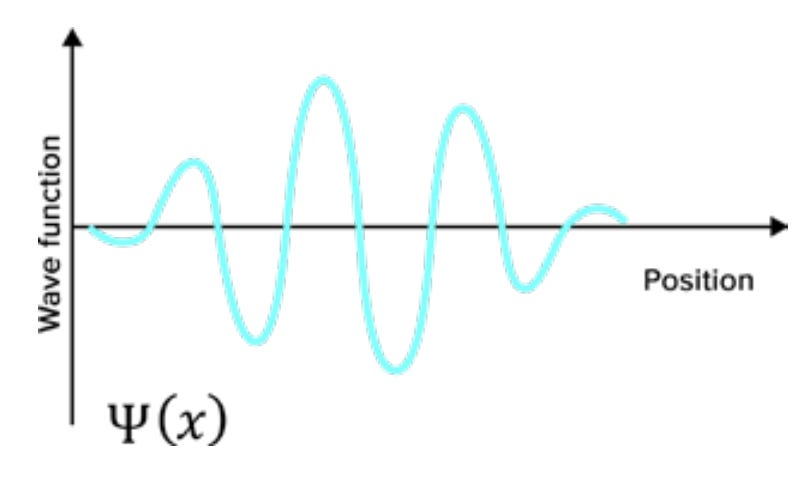
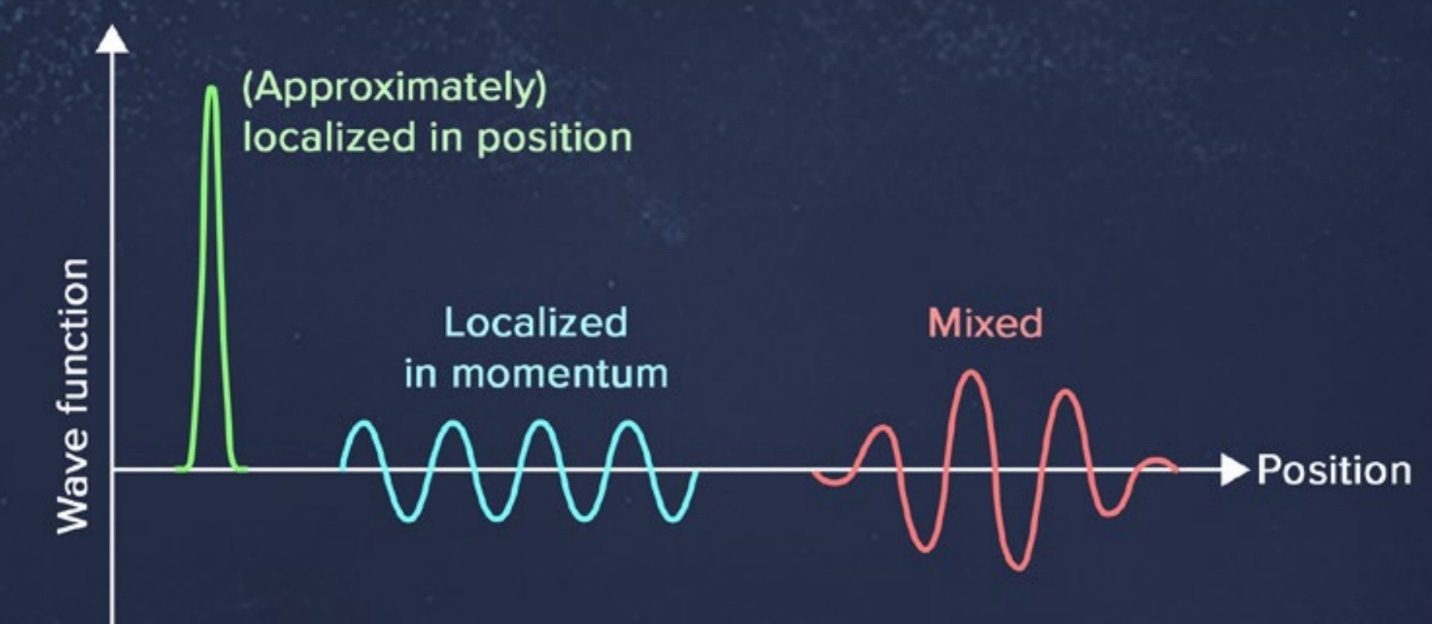
In classical mechanics, the state of a particle is not specified by only giving its position, x. You also need to specify the momentum, p, which is mass times velocity: p = mv. So, if you know where a particle is in classical mechanics but don’t know how fast it’s moving, you can’t predict anything about where it’s going to be next. You don’t know what direction it’s moving in. But in quantum mechanics, the wave function doesn’t depend on position and momentum separately—it only depends on the position. So, in quantum mechanics—as a successor theory to classical mechanics—where is the information about momentum in the quantum wave function? How do you know what you’re going to observe about the momentum, p? The answer is that you can also define a wave function that depends on the momentum. You can call it Ψ(p) as opposed to Ψ(x). Ψ(x) is the position wave function, whereas Ψ(p) is the momentum wave function. And the momentum wave function will tell you the probability of measuring the momentum to have any particular value in the usual way: You take the square of the modulus (that is, the amplitude squared), and that gives you the probability … [Y]ou can talk separately about the position wave function, which tells you the probability of any position measurement, and the momentum wave function, which tells you the probability of a momentum measurement. The trick is that the momentum wave function is not defined separately from the position wave function. In classical mechanics, position and momentum are independent. In quantum mechanics, the position wave function is equivalent to the momentum wave function. There is a well-defined mathematical way of going back and forth, and it’s called the Fourier transform. Neither the position wave function nor the momentum wave function by itself is fundamental. There is a single thing—call it the quantum state— that’s an abstract state of description, and it’s just that the quantum state can be expressed equally well as a wave function depending on position or as a wave function depending on momentum. Classically, knowing the position of a particle tells you nothing about its momentum, and vice versa, whereas quantum mechanically, there’s a single quantum state that tells you everything there is to know about both position and momentum. How does that work? The answer is there’s an interesting relationship between these two ways of expressing the quantum state: the position wave function and the momentum wave function. If the position wave function is highly localized—if Ψ(x) is almost entirely concentrated around some particular point in space such that you know that if you measure, that’s probably where you’re going to see it—then the Fourier transform, or the map from position wave functions to momentum wave functions, tells you that the momentum wave function will be spread out all over. If you were to measure the position of a particle with a highly localized wave function, you’d have a pretty good idea ahead of time where you’re going to find it. But if you take that same particle with the same wave function, and want to measure its momentum, you have no idea what answer you would get. There are many different possibilities, all of which would have substantial probability for getting that answer. Likewise, the other way around works just as well. If you have a momentum wave function that is localized around some value—so you know essentially what you would get if you measured the velocity or momentum of the particle—then the position version of the wave function is spread out all over, so you have no idea what position you would measure for that kind of particle. There are also wave functions that are neither exactly localized in position or momentum—they’re compromises. They are somewhat compact with respect to position and somewhat compact with respect to momentum. In that case, there’s uncertainty about what you would measure if you measured either the position or the momentum.

None of these options lets you say that if you measure either one, you can predict carefully what you are going to observe. This feature is the heart of the uncertainty principle: You can have a wave function that is localized in position, and you can have a wave function that is localized in momentum. You cannot have both at the same time. There is an unavoidable trade-off in how compact a wave function can be in both position and momentum at once. Notice that it has not been stated that in quantum mechanics, measuring the position disturbs the system and leaves its momentum uncertain, or vice versa. It’s true that when you measure a system, you can collapse the wave function and change it—but that’s not the fundamental point of the uncertainty principle. The uncertainty principle is not a statement about measurements, though it might imply things about measurements. It’s a statement about what kinds of wave functions can possibly exist. You can measure either position or momentum. That’s your choice as an experimentalist. And if you’re a good experimentalist, you’re going to get a well-defined answer: You’re going to see the electron having a position or see it having a momentum, depending on your experiment. But there are no wave functions where both quantities are precisely defined at the same time ahead of time. So, is the wave function all there is? That’s the reality problem. Or does an electron really have a well-defined position and momentum even before you measure it, but somehow quantum mechanics doesn’t know how to describe those real-world quantities?

Regarding what we can describe through experiments that have been conducted, Carroll writes:

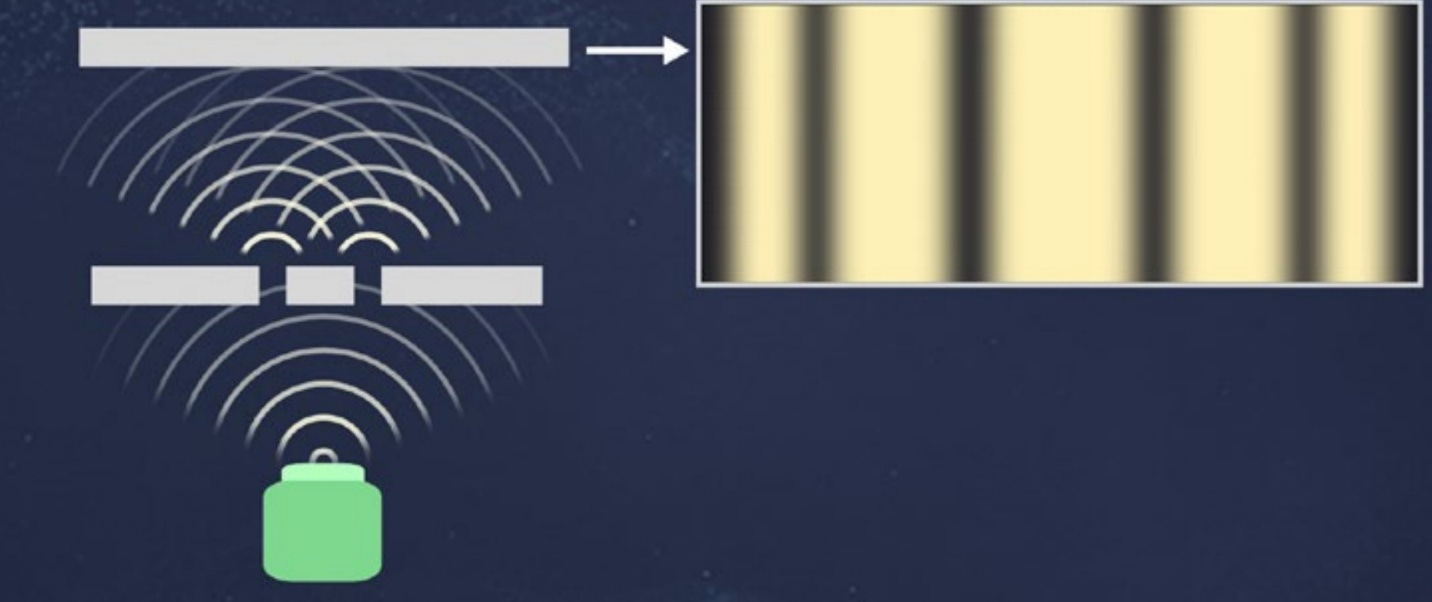
One good way to get into these issues is to consider yet another famous thought experiment in quantum mechanics: the double-slit experiment. Picture a tub of water. If the water is perfectly still and you poke it, ripples will emanate outward from where you poked it. They’ll move in a circular pattern, getting farther and farther away. Then, imagine that you put a barrier into the water some distance away from where you start the ripples. If there is a single slit in the barrier, then some waves are going to pass through. On the other side of the barrier, the waves will again emanate from the slit in another semicircular pattern. Now imagine that there are two slits in the barrier. Then, two circular patterns of ripples will emerge on the other side. And you’ve learned that when you have waves, you can have interference. So, these ripples coming out of the two slits will interfere. At some points, they will reinforce each other— points where the two ripples are moving in the same direction—and at some points, they will cancel each other out. Next, consider doing this with light rather than water. Take a beam of light pointed at a thin slit in a barrier and set up a detector on the other side. If you start with a single slit, then because light has wavelike properties, you will see the light spread out a bit. That’s diffraction. It won’t quite be a semicircle because the light has some momentum in that direction. Then, imagine you have a barrier with two slits that are pretty close together—not much farther apart than the wavelength of the light. Then, at a detector placed on the opposite side, you see an interference pattern: bright bands with dark bands in between. Given the distances from the source of light to the slits to the detector, the light waves will interfere either constructively (build up) or destructively (cancel each other out). This version of the double-slit experiment was done by Thomas Young in the 19th century to demonstrate the wave nature of light.

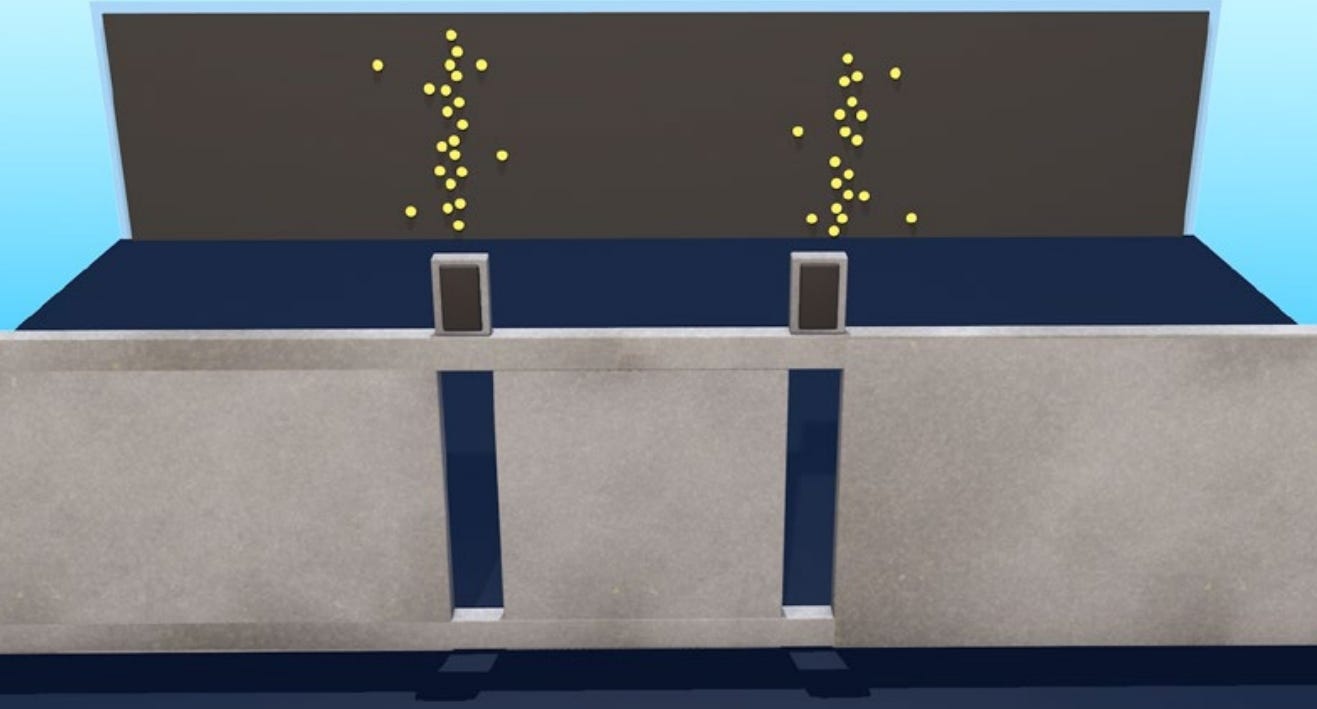
If you instead send particles through the slits, some of the particles will hit the barrier and then stop, while others will pass through the slit. But if they get lucky enough to pass through the slit, they’re just going to continue in a straight line. Classically, particles do not diffract; they keep moving unless they hit something. Mostly, a particle detector on the other side of the two slits will basically see the slits: It will measure a bunch of detected particles in a single location for a single slit. If there are two slits, there will be two bunches in two locations. You don’t get interference patterns by sending particles through double slits. Particles don’t interfere with each other. Particles have a location in space; they do not spread out everywhere. Returning to the double-slit experiment using light, imagine you make the intensity of the light beam extremely small. When you make the light that dim, you eventually stop seeing a continuous image at the detector. Rather, you start detecting individual flashes at specific locations. This is because you’ve reached the realm of individual photons. What you thought for bright light was a wave passing through the slits, you now realize that when the light gets very dim, it’s actually a collection of individual photons. So, a sensitive photodetector—a machine that discovers photons when they get hit by photons—can measure photons one at a time. High-intensity light shows wavelike interference patterns, but low-intensity light behaves like point-like particles. How can that be reconciled? The answer comes if you look at the individual flashes from low-intensity light. Any individual photon leaves a flash, but if you allow those flashes to accumulate over time, the flashes are detected one by one by the detector— but they do not congregate around just two points, one for each slit. Rather, the photon dots that show up in the detector cluster in high-intensity bands separated by low-intensity empty regions and then fall away if you get far away from where the slits are pointing. In other words, photons do exhibit interference patterns—even when you’re viewing them one at a time as individual particles. And the same behavior holds for electrons. This was a thought experiment for a long time, but the experiment can actually be done … [I]t wasn’t until 2012 that physicists could do the experiment in a laboratory. If you send a single electron through two slits, the detector on the other side will see a dot like a particle. But—just like light—if you keep sending electrons through one at a time, many dots will accumulate, and that accumulation of dots will look like an interference pattern.

If classical physics were right and electrons were just particles, this is very hard to make sense of. You’re sending electrons through one at a time, yet their accumulated effect is an interference pattern that seems wavelike. This means that each electron must somehow be interfering with itself. So, it knows not to go to the places where the interference bands are dark; it knows to probably go where the interference bands are light. And if you insist on thinking of the electron as an ordinary particle—which you shouldn’t—that electron either went through one slit or the other one. A particle cannot go through both. So, how did it interfere with itself? Within quantum mechanics, the answer is that the electron is a wave function. When it’s passing through two slits, there is absolutely something wavelike. Wave functions have no trouble interfering with themselves. And then it’s only when the electron is finally detected on the other side that it looks like a particle. That’s the short motto for quantum mechanics: It’s a wave when you’re not looking at it; it looks like a particle when you do. If you wanted to stubbornly insist that the electron went through either one slit or the other, you could presumably find out by placing small detectors near the slits to measure which slit the electron goes through. For every electron you fire at the slits, you detect that it goes through one slit—not two. It looks like a particle, and then it continues on to be detected on the other side. When you detect it, it always looks like a particle when you observe it. But if you send many electrons through and monitor which slit they go through, each electron only goes through one or the other each time. And on the other side, where you have the main detector, the interference pattern goes away. When you try to figure out which path the electron takes, you force it to take one or the other. The wave function collapses onto whichever slit you observed it to go through. So, your observation has fundamentally changed the state of the system. The double-slit experiment seems to have implications for the question of whether the wave function represents something real or whether it should be thought of as something epistemic. Philosophers use the word epistemic to refer to knowledge or the ability to make predictions.

What could possibly cause the wave function to “collapse”?  That is a fundamental, as-yet-unanswered question.  “Decoherence theory” offers a general explanation by suggesting that interactions with the environment cause the wave function to appear to collapse. That is, when a quantum system interacts with its larger environment, the superpositions of the system become “entangled” with the states of the environment. This interaction leads to the loss of coherence between the components of the superposition (“decoherence”), making the system appear classical and thus effectively collapsing the wave function.  But no one has been able to pinpoint exactly at which point a surrounding environment can “overwhelm” a quantum system and thereby cause it to behave under the rules of classical physics.  (The Copenhagen interpretation of this phenomenon posits that the wave function collapse is a fundamental process that occurs during measurement, but offers no causal explanation of why that happens.  On the other hand, the “Many-worlds” interpretation of this phenomenon posits that all possible outcomes of a quantum measurement actually occur, each in a separate, branching universe, such that there is no collapse, but instead the universe splits into multiple copies.  Pretty wild.)

Carroll (himself a proponent of the “Many-worlds” interpretation) continues:

The double-slit experiment implies that the electron isn’t simply described by a wave. It seems to legitimately act like a wave when you’re not observing it. It’s not just that individual electrons go through one slit or the other and you just don’t know. The correct thing to say is that the wave function of the electron goes through both slits. You need to be able to say that because that’s how the electron is able to interfere with itself—by being a wave when it goes through those two slits. At least at face value, this kind of behavior is what makes people think that the wave function should be thought of as a real thing, not just a way of making predictions. A physical, actual wave has no problem interfering with itself. But something that you just think of as a tool for making predictions— how does that interfere with itself? Bohr, Heisenberg, and colleagues decided that wave functions should not be thought of as directly representing reality. The fact that you don’t observe wave functions directly lends that view some credence. If the wave functions were the real physical stuff of the world, why can’t you just measure them? Why do they keep collapsing every time you look? Many intelligent physicists today still don’t think of wave functions as representing reality. But quantum mechanics is confusing. You should be open to different possibilities, and phenomena like the double-slit experiment suggest that you should at least take seriously the possibility that the wave function does represent reality. This is called the realist position about the wave function.

We can’t yet know (and may never know) what exactly explains the causal mechanism behind the results we see from quantum mechanics.  But humankind has come a long way in our understanding, as will be explored in the next essay in this series.

Links to other essays in this series: Part 1; Part 2; Part 3; Part 4; Part 5; Part 6.