The Physical Universe – Part 3

Thermodynamics.

Continuing this essay series on the physical universe, this essay will explore thermodynamics, which explains how large quantities of particles interact, including how energy’s ability to organize things dissipates over time (that is, energy can only do less useful work over time), which in turn explains how time only moves in one direction.

As Jim Al-Khalili writes in The World According to Physics:

In physics, the concept of energy indicates the capacity to do work; thus, the more energy something has, the more it is able to do, whether that ‘doing’ means moving matter from one place to another, heating it up, or just storing the energy for later use … Let us begin with the law of conservation of energy, which states that the total amount of energy in the universe is constant … On the face of it, you might think that this is all there is to it: the total amount of energy in a system (indeed, in the entire universe) is conserved, even though it changes from one form to another. But there is something deeper about the nature of energy that I have not yet mentioned. In a rather loose sense, we can divide it into two types: useful energy and waste energy—a distinction that has profound consequences linked to the arrow of time. We know we need energy to run our world, to feed our transport and our industries, to generate the electricity we use to light and heat our homes, to run our appliances and to power all our electronic devices. Indeed, energy is required just to sustain life itself. Surely this cannot last forever. So, will we one day run out of useful energy? Zooming out, we can think of the entire universe as a wound-up mechanical clock that is slowly running down. But how can this be so if energy is always conserved? Why can’t energy circulate indefinitely, changing from one form to another, but always there? The answer turns out to be down to simple statistics and probability, and what is known as the second law of thermodynamics.

In thermodynamics, temperature is a measure of the thermal energy of a system. In statistical mechanics generally, the energy is the average kinetic energy of the particles.  Speaking of statistical mechanics generally, Al-Khalili writes:

So, if we want to understand the physics of the world we see around us, we need to understand how particles interact and behave in large collections. The area of physics that helps us to understand the behaviours of large numbers of interacting bodies is statistical mechanics … [A bouncing] ball loses its bounce for the same reason that heat always flows from a warm cup of coffee to the colder surrounding air and never back again, and why the sugar and cream in the coffee never un-dissolve and un-mix. Welcome to the field of thermodynamics — the third major pillar of physics (along with general relativity and quantum mechanics). While statistical mechanics describes how a large number of particles interact and behave in a system, thermodynamics describes the heat and energy of the system and the way these change over time.

Al-Khalili then discusses the concept of entropy, which measures a system’s capacity to do work in the form of organizing things together (if a system is “high entropy,” it has a low capacity to organize things; if a system is “low entropy,” it has a high capacity to organize things):

A more interesting definition of entropy is as a measure of something’s ability to expend energy in order to carry out a task. When a system reaches equilibrium, it becomes useless. A fully charged battery has low entropy, which increases as the battery is used. A discharged battery is in equilibrium and has high entropy. This is where the distinction between useful energy and waste energy comes in. When a system is ordered and in a special (low-entropy) state, it can be used to carry out useful work—like a charged battery, a wound-up clock, sunlight, or the chemical bonds between carbon atoms in a lump of coal. But when the system reaches equilibrium, its entropy is maximised, and the energy it contains is useless. So, in a sense, it is not energy that is needed to make the world go around, it is low entropy. If everything were in a state of equilibrium, nothing would happen. We need a system to be in a state of low entropy, far from equilibrium, to force energy to change from one form to another—in other words, to do work. We consume energy just by being alive, but we can see now that it has to be of the useful, low-entropy kind. Life is an example of a system that can maintain itself in a state of low entropy, away from thermal equilibrium. At its heart, a living cell is a complex system that feeds (via thousands of biochemical processes) on useful, low-entropy energy locked up in the molecular structure of the food we consume. This chemical energy is used to keep the processes of life going. Ultimately, life on earth is only possible because it ‘feeds’ off the Sun’s low-entropy energy.

The universe’s relentless overall move to a higher entropy state means time can only move in one direction (for example, heat spontaneously flows from hot to cold objects, not the reverse, and this increases the overall entropy of the system; the universe as a whole is slowly moving towards thermodynamic equilibrium, a state in which entropy is maximized and no more useful energy is available to do work):

Imagine watching a movie of our box of air (and let us imagine that the molecules of air are big enough for us to see). They will be bouncing around, colliding with each other and with the walls of the box, some of them moving faster and others slower. But if the air is in thermal equilibrium, then we would not be able to tell whether the movie is being run forwards or backwards. Down at the scale of molecular collisions, we cannot see any directionality to time. Without an increase in entropy and a drive to equilibrium, all physical processes in the universe could happen equally well in reverse. However, as we saw, this tendency of the universe and everything in it to unwind towards thermal equilibrium is entirely down to the statistical probability of events at the molecular level progressing from something less likely to happen to something more likely, according to the laws of thermodynamics. The directionality of time pointing from past to future is not mysterious; it’s just a matter of statistical inevitability. With that in mind, even the fact that I know the past but not the future is no longer so strange. As I perceive the world around me, I increase the amount of information stored in my brain, a process which, as my brain is doing work, produces waste heat and increases my body’s entropy.

Peter Atkins explores this is more detail in his concise book The Laws of Thermodynamics: A Very Short Introduction.  As Atkins writes:

Among the hundreds of laws that describe the universe, there lurks a mighty handful. These are the laws of thermodynamics, which summarize the properties of energy and its transformation from one form to another … Do not think that thermodynamics is only about steam engines: it is about almost everything. The concepts did indeed emerge during the nineteenth century when steam was the hot topic of the day, but as the laws of thermodynamics became formulated and their ramifications explored it became clear that the subject could touch an enormously wide range of phenomena, from the efficiency of heat engines, heat pumps, and refrigerators, taking in chemistry on the way, and reaching as far as the processes of life.

As Atkins explains, assessing the effects of thermodynamics requires focusing on a smaller system:

The part of the universe that is at the centre of attention in thermodynamics is called the system. A system may be a block of iron, a beaker of water, an engine, a human body. It may even be a circumscribed part of each of those entities. The rest of the universe is called the surroundings. The surroundings are where we stand to make observations on the system and infer its properties … A system is defined by its boundary. If matter can be added to or removed from the system, then it is said to be open. A bucket, or more refinedly an open flask, is an example, because we can just shovel in material. A system with a boundary that is impervious to matter is called closed. The properties of a system depend on the prevailing conditions. For instance, the pressure of a gas depends on the volume it occupies, and we can observe the effect of changing that volume if the system has flexible walls. ‘Flexible walls’ is best thought of as meaning that the boundary of the system is rigid everywhere except for a patch—a piston—that can move in and out. Think of a bicycle pump with your finger sealing the orifice. Suppose we have two closed systems, each with a piston on one side and pinned into place to make a rigid container (Figure 1). The two pistons are connected with a rigid rod so that as one moves out the other moves in. We release the pins on the piston. If the piston on the left drives the piston on the right into that system, we can infer that the pressure on the left was higher than that on the right, even though we have not made a direct measure of the two pressures.

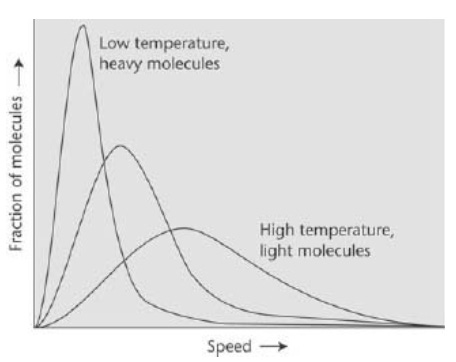
[I]t turns out that the average speed of the molecules increases as the square root of the absolute temperature. The average speed of molecules in the air on a warm day (25°C, 298 K) is greater by 4 per cent than their average speed on a cold day (0°C, 273 K). Thus, we can think of temperature as an indication of the average speeds of molecules in a gas, with high temperatures corresponding to high average speeds and low temperatures to lower average speeds.

The figure above shows the Maxwell-Boltzmann distribution of molecular speeds for molecules of various mass and at different temperatures. Note that light molecules have higher average speeds than heavy molecules. The distribution has consequences for the composition of planetary atmospheres, as light molecules (such as hydrogen and helium) may be able to escape into space.

Atkins then discusses the first law of thermodynamics:

The first law of thermodynamics is generally thought to be the least demanding to grasp, for it is an extension of the law of conservation of energy, that energy can be neither created nor destroyed. That is, however much energy there was at the start of the universe, so there will be that amount at the end. But thermodynamics is a subtle subject, and the first law is much more interesting than this remark might suggest … [T]he first law motivates the introduction and helps to clarify the meaning of the elusive concept of ‘energy’ … All we shall assume is that the well-established concepts of mechanics and dynamics, like mass, weight, force, and work, are known. In particular, we shall base the whole of this presentation on an understanding of the notion of ’work’. Work is motion against an opposing force. We do work when we raise a weight against the opposing force of gravity. The magnitude of the work we do depends on the mass of the object, the strength of the gravitational pull on it, and the height through which it is raised. You yourself might be the weight: you do work when you climb a ladder; the work you do is proportional to your weight and the height through which you climb … With work a primary concept in thermodynamics, we need a term to denote the capacity of a system to do work: that capacity we term energy. A fully stretched spring has a greater capacity to do work than the same spring only slightly stretched: the fully stretched spring has a greater energy than the slightly stretched spring. A litre of hot water has the capacity to do more work than the same litre of cold water: a litre of hot water has a greater energy than a litre of cold water. In this context, there is nothing mysterious about energy: it is just a measure of the capacity of a system to do work, and we know exactly what we mean by work … Now we do some experiments. First, we churn the contents of the flask (that is, the system) with paddles driven by a falling weight, and note the change in temperature this churning brings about. Exactly this type of experiment was performed by J. P. Joule (1818-1889), one of the fathers of thermodynamics, in the years following 1843. We know how much work has been done by noting the heaviness of the weight and the distance through which it fell. Then we remove the insulation and let the system return to its original state. After replacing the insulation, we put a heater into the system and pass an electric current for a time that results in the same work being done on the heater as was done by the falling weight. We would have done other measurements to relate the current passing through a motor for various times and noting the height to which weights are raised, so we can interpret the combination of time and current as an amount of work performed.

As Jeffrey Gross writes in Thermodynamics: Four Laws That Move the Universe:

The first law of thermodynamics states the energy conservation principle: Energy can neither be created nor destroyed, but only converted from one form to another. Energy lost from a system is not destroyed; it is passed to its surroundings. The first law of thermodynamics is simply a statement of this conservation.

The first law is fundamental to the study of heat engines, which convert heat into work. The efficiency of a heat engine is determined by how well it can convert the input heat into useful work without too much heat being lost to the external environment (and being wasted).  As Atkins writes:

[T]he molecular interpretation of heat and work elucidates one aspect of the rise of civilization. Fire preceded the harnessing of fuels to achieve work. The heat of fire—the tumbling out of energy as the chaotic motion of atoms—is easy to contrive for the tumbling is unconstrained. Work is energy tamed, and requires greater sophistication to contrive. Thus, humanity stumbled easily on to fire but needed millennia to arrive at the sophistication of the steam engine, the internal combustion engine, and the jet engine.

When we consider the second law of thermodynamics, we come to understand why time only moves in one direction.  To see this, one needs to consider why no process using energy is reversible.  As Grossman explains:

A reversible process is not real: It is an idealized process for which the following conditions all hold throughout the entire process. First, the system is always in equilibrium. Second, there are no dissipative processes occurring (in other words, no energy is lost to the surroundings—there’s no friction, viscosity, electrical resistance, and so on). Finally, a reversible process can occur both forward and backward with absolutely no change in the surroundings of the system.

But of course, most natural processes are irreversible, meaning they can’t be reversed without leaving a change in the system or the surroundings. For example, the presence of friction means that some heat will always be wasted when energy is used to do work.  That leads to the second law of thermodynamics, which states that the total entropy of an isolated system always increases over time for irreversible processes.  Another example of the second law of thermodynamics in application is a refrigerator.  A refrigerator always emits more heat than the electrical energy it uses: the refrigerator removes heat from its interior (the cold space) to keep the food and other items cool; to move this heat from the inside to the outside (against the natural direction of heat flow), the refrigerator uses electrical energy; the refrigerator then releases the heat it removed from the inside plus the electrical energy it used to do this work to the surroundings (the area around the refrigerator, particularly the back where the coils are located, feels warm).

As Grossman writes, “We can think about entropy as the property that measures the amount of irreversibility of a process. If an irreversible process occurs in an isolated system, the entropy of the system always increases.”

The laws of thermodynamics therefore predict that as the universe continues to expand, it will cool down.  Galaxies will move farther apart, stars will exhaust their nuclear fuel and die, leading to a universe dominated by darkness and cold.  At that point, entropy will reach its maximum value, and the universe will be in thermodynamic equilibrium, with no temperature differences to drive energy flow or sustain processes that require work.

But don’t worry.  That result is 10 to the one hundredth power years from now away.  In the mean time, there’s much work to be done!

In the next essay in this series, we’ll explore the strange and fascinating results of quantum mechanics, which operates at the subatomic level.

Links to other essays in this series: Part 1; Part 2; Part 3; Part 4; Part 5; Part 6.