The Physical Universe – Part 1

Spacetime.

In this series of essays, we’ll explore the world of physics and its profound impact on our lives.  Indeed, since everything in the universe operates according the laws of physics, there can be no more fundamental understanding of underlying reality.  During the COVID lockdowns, my kids (and my older son in particular) loved the documentaries by Jim Al-Khalili, and recently I came across his wonderful summary of physics, The World According to Physics.

As Al-Khalili writes:

[T]he wonders of our universe can and should be appreciated by everyone, and gaining a basic understanding doesn’t take a lifetime of study … To convey a working knowledge of what physics tells us about the nature of our world, I have selected an array of the most important concepts in modern physics and attempted to show how they link together … A perfect example of the search for simplicity is science’s long and continuing journey to discover the basic building blocks of matter. Take a look around you. Consider the sheer range of materials that make up our everyday world: concrete, glass, metals, plastics, wood, fabrics, foodstuffs, paper, chemicals, plants, cats, people … millions of different substances, each with its own distinctive properties: squidgy, hard, runny, shiny, bendy, warm, cold … If you knew nothing of physics or chemistry, you might imagine that most materials have little in common with each other; and yet we know that everything is made of atoms, and that there is only a finite number of different kinds of atoms … [A]ll the stuff making up our world, including our own bodies, and including everything we see out in space—the Sun, the Moon, and the stars—is all made of fewer than a hundred different types of atoms. We also now know that atoms have internal structure. They are made of tiny, dense nuclei surrounded by clouds of electrons while the nucleus itself is made up of smaller constituents: protons and neutrons, which are in turn made of even more fundamental building blocks called quarks … As we understand physics today, all the matter we see in the world is made up of not the four classical elements of the Greeks, but just three elementary particles: the ‘up’ quark, the ‘down’ quark, and the electron. That’s it. Everything else is just detail … And yet the job of physics is more than just classifying what the world is made of. It is about finding the correct explanations for the natural phenomena we observe and the underlying principles and mechanisms that account for them.

People tend to gravitate toward symmetrical things (I notice children like to draw things symmetrically), and nature reflects that tendency as well:

The universality of the laws of nature has fascinating mathematical origins and is linked with one of the most powerful ideas in science: symmetry. At a rudimentary level, everyone understands what is meant by a geometric shape that is symmetrical. A square is symmetrical because if you draw a line vertically down its centre, splitting it in half (or doing the same thing with a horizontal or diagonal line), then swapping the two halves around doesn’t alter its shape. You also achieve the same result if you rotate it in multiples of 90 degrees. A circle has even more symmetry, because you can rotate it by any angle without changing its appearance. In physics, symmetries can tell us something much deeper about reality than just the invariance of certain shapes when they are rotated or flipped. When physicists say that a physical system has a symmetry, they mean that some property of that system stays the same when something else changes. This turns out to be a very powerful concept. ‘Global’ symmetries are when laws of physics remain the same (there is no change in the way they describe some feature of the world) as long as some other change, or ‘transformation’, is applied equally everywhere. In 1915, Emmy Noether discovered that, wherever we see such a global symmetry in nature, we can be sure to find an associated law of conservation (a physical quantity remaining the same). For example, the fact that the laws of physics don’t change when you move from one place to the next gives us the law of conservation of momentum, and the fact that the laws of physics don’t change from one time to the next gives us the law of conservation of energy … This has proven to be an extremely useful idea in theoretical physics and has deep philosophical consequences. Physicists are always on the lookout for deeper, less obvious symmetries that are hidden in their mathematics. Noether’s theorem tells us that we don’t ‘invent’ the mathematics in order to have a way of describing the world, but rather, as Galileo observed, that nature speaks the language of mathematics, which is ‘there’, ready and waiting to be discovered.

Al-Khalili also describes the nature of “emergence,” by which larger principles are required to make sense of the operation of many smaller things in the aggregate:

We can study the properties of a molecule of H2O as much as we want: the geometry of the bonds between the oxygen and hydrogen atoms and the quantum rules that govern this, the way water molecules stick together and arrange themselves, and so on. But we would not be able to deduce the property of ‘wetness’ of water by looking solely at its constituent parts down at the molecular level. This ‘emergent’ property only becomes apparent when trillions of water molecules come together in bulk. Does this then imply that the whole is more than the sum of its parts, in the sense that there is some extra physics that we need to include to explain, for example, the bulk properties of matter? Not necessarily. The idea of emergence—that there are qualities of the physical world, like heat or pressure or the wetness of water, that do not have counterparts at the level of atomic physics—does not mean that there is more to a system than the sum of its parts, provided those emergent properties are still only built upon more fundamental concepts, such as the electromagnetic forces between subatomic particles in the case of water. The reductionist enterprise continued when physicists in the nineteenth century attempted to understand the properties of complex systems that could not be explained by the simple laws of Newtonian mechanics. Towards the end of that century, James Clerk Maxwell and Ludwig Boltzmann developed two new subfields of physics—thermodynamics and statistical mechanics—which helped physicists to learn about systems made up of many pieces by looking at them ‘in bulk’ … Thus, while it is true that we cannot measure the temperature or pressure of a gas by looking at how its individual molecules vibrate and bump into each other, we still know that temperature and pressure are due to nothing more than the collective behaviour of individual molecules. What else can there be? But while this simplistic reductionist line of thinking is not wrong—in the sense that there is no extra physical process that magically appears when we zoom out from the molecular scale—it is of limited usefulness when trying to describe the properties of a complex system. What we require is not ‘new’ physics, but ‘more’ physics, in order to learn about and understand how certain properties can emerge in a system from the collective behaviours of its constituents.

Al-Khalili continues:

But knowing that more physics is needed when we put the constituent parts (the particles, atoms and molecules) together to make up bulk matter is not the same as saying we know what that missing physics is. This becomes clear if we try to find a unified picture of the physical universe. We are still unable to derive the laws of thermodynamics from the Standard Model of particle physics, for example—or indeed to do the reverse, since it is not obvious which of these two pillars of physics is the more fundamental. And we are even further away from understanding more-complex structures, such as what distinguishes life from non-life. After all, you and I are still only made up of atoms, yet being alive is clearly more than just a matter of complexity, for a living organism is no more complex in terms of its atomic structure than an identical but recently deceased organism … And yet … maybe we can dream of a time when we are able to have a single unified physical theory that underpins all natural phenomena. Until then, suffice it to say, a reductionist line of thinking only gets us so far, and we need to use different theories and models depending on what we are trying to describe.

As Al-Khalili writes, the project of a universal explanation of all physical laws has hit a speedbump in modern times in the form of quantum physics, the strange subatomic world that we now know is governed by principles that shock our common, macro-world senses:

Despite our quest for laws of physics that are universal, the limits of reductionism point to the fact that sometimes the world can behave very differently at different scales and needs to be described and explained using the appropriate model or theory. For example, on the scale of planets, stars, and galaxies, gravity dominates everything—it controls the structure of the cosmos. But it plays no role, that we can detect, down at the atomic scale where the other three forces (electromagnetism and the strong and weak nuclear forces) dominate. Indeed, probably the biggest unresolved problem in the whole of physics … is that the laws of physics that describe our everyday, so-called ‘classical’ world of matter, energy, space, and time simply don’t work when we shrink down to the world of individual atoms, where the very different rules of quantum mechanics come into play.

Stepping back to the most basic level of space and time itself, Al-Khalili describes how Albert Einstein took something Isaac Newton had simply assumed, and showed how those assumptions were wrong:

In order to paint Einstein’s picture of the world, we must start with the canvas itself. Space and time are the substrates in which all events take place. However, such concepts are slippery. Common sense tells us that space and time should be in place from the start—that space is where events happen and the laws of physics are acted out, while the inexorable passage of time is, well, just is. But, is our commonsense view of space and time right? An important lesson physicists must learn is to not always trust common sense. After all, common sense tells us that the Earth is flat, but even the Ancient Greeks understood that its sheer size meant we could not easily discern its curvature, but that there were simple experiments they could perform to prove that it was in fact a sphere … When it comes to the meaning of space and time the difficulty we have is not surprising, for we are ourselves imprisoned within them, and it is hard to free our minds from their confines and ‘see’ reality from the outside. And yet, incredibly, this is possible to do … I will outline our current understanding of the nature of space and time—a celebration of the debt we owe to Einstein and his two beautiful theories of relativity.

Al-Khalili first describes Einstein’s relativity of simultaneity, as follows:

Einstein proved that absolute space and absolute time do not exist as separate entities. But to appreciate why this notion is necessary, I need to introduce you to the first of his two theories of relativity … Newton described how objects move and behave under the influence of forces, and since all motion or change requires time to make any sense, time had to be included as a fundamental part of his mathematical description of the world. But Newtonian time is absolute and relentless; it flows at a constant rate, as though there were an imaginary cosmic clock ticking off the seconds, hours, days, and years independently of the events and processes taking place in space. Then, in 1905, Einstein brought the Newtonian world crashing down by revealing how time is connected to space at a deep level. Einstein’s conclusion was that time is not absolute: it doesn’t run at the same rate for everyone. If I see two simultaneous events—say, two flashes of light from sources on either side of me—then someone else moving past me at that very moment will not see them happening at the same time, but rather one slightly after the other. This is because the rate of flow of time for each of us depends on our state of motion relative to each other. This weird notion is one of the very first lessons of relativity theory and is called the relativity of simultaneity. Let us take a step back and look at these concepts more carefully. Consider how sound waves travel to your ears. Sound is, after all, nothing more than the vibration of air molecules that pass on energy through their collisions. Without matter (air) there would be no sound … Einstein’s insight was to suggest that, unlike sound waves, light waves do not need a medium to carry them. His theory rested on two ideas (known as the principles of relativity). The first, originating with Galileo, states that all motion is relative and that there is no experiment that can be performed to show that someone or something is truly at rest. The second principle states that light waves travel at a speed that is independent of the speed of the source of the light. Both these ideas seem reasonable, until you dig a little deeper into their implications. Let us consider the second idea first—that light moves at the same speed for everyone—and carry out a simple thought experiment.

Al-Khalili then describes the thought experiment that led Einstein to his discovery that the speed of light, unlike all other things, is the same regardless of the speed of the things measuring it:

Imagine an approaching car on an empty country road. The sound waves from its engine will reach you ahead of the car since they are travelling faster, but their speed has to do with how quickly the vibrating air molecules can transmit them; they do not reach you any quicker if the car speeds up. What happens instead is that they get compressed to shorter wavelengths. This is the well-known Doppler effect that we recognise as the change in pitch of the car as it finally reaches you and goes past. When it is receding, the waves of sound are emitted from a progressively longer distance away and therefore reach us stretched to longer wavelengths, and hence a lower pitch. So, while the wavelength of sound waves depends on the speed of their source, the speed of the waves themselves relative to us (how long they take to reach us) does not change unless we start moving through the air towards the approaching car. So far, so good, I hope. Light is different. It does not need a medium to travel through, and with respect to which we can measure its speed. This means that no one has a privileged position in which they can say they are truly at rest and therefore can reliably measure the ‘true’ speed of light. Einstein concluded from this that we should all measure light to have the same speed regardless of how fast we are moving relative to each other. Now consider two rockets approaching each other at constant speed close to that of light. But they have no reference point to argue over who is, or isn’t, moving. An astronaut on board one rocket sends a pulse of light towards the oncoming second rocket, measuring the speed of the pulse as it travels away from him. Since he can quite legitimately claim to be at rest, floating in empty space, while the other rocket is doing all the moving, he should see the light moving away from him at its usual speed of just over one billion kilometres per hour, and he does indeed see this. But at the same time, the astronaut in the second rocket can also legitimately claim to be floating stationary in space. She too will therefore expect to measure the speed of the light reaching her to be just over one billion kilometres per hour (since, like the sound waves from the car, the light’s speed should not depend on the speed that its source is approaching her). And she does indeed measure light to have this speed. It would seem, therefore, that both astronauts measure the same light pulse to be travelling at the same speed, despite moving towards each other themselves at near light speed! This strange nature of light turns out to be a property of the speed at which it can travel rather than of light itself— a speed that is the maximum possible in our universe and which stitches space and time together into one fabric. For the only way light can travel at the same speed for all observers regardless of how fast they themselves are moving relative to each other is if our concepts of distance and time change … Here is another example. Imagine that you, on Earth, send out a series of light pulses, or flashes, into space to chase down a friend who has headed off in a very fast rocket—a powerful futuristic one that can travel at 99 percent of the speed of light. You will measure the light pulses to be travelling away from you at one billion kilometres per hour and therefore slowly overtaking your friend’s rocket at just 1 percent of the speed of light, in the same way that a car in the fast lane of a motorway that is travelling just a little faster than one in the slow lane overtakes it at a speed that is the difference between their two speeds. But what does your friend in the rocket see if she tracks the overtaking light pulses? Relativity theory tells us that she will see them overtaking her at one billion kilometres per hour. Remember, the speed of light is constant, and all observers see it travelling at the same speed. The only way for this to make sense is if time on board the rocket is ticking by at a slower pace than for you on Earth. That way, what you see as the slow overtaking of a light pulse past the rocket window, your friend sees as a light pulse flashing past, because very little time will have elapsed on the rocket’s slower-ticking clock—although for your friend, the clock is ticking at a normal rate. Thus, one of the consequences of all observers seeing light moving at the same speed is that we all measure distances and times differently. And we do indeed see this: the constancy of the speed of light for all observers is a fact, verified experimentally over and over again, and without which our world wouldn’t make sense.

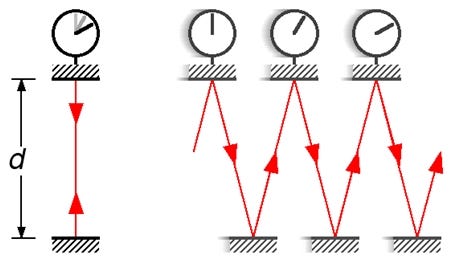
Another way of explaining why the faster you travel through space, the slower you travel through time, is as follows:

Imagine a light clock (between two mirrors the light bounces up and down and the time it takes from one to the other is one tick). One is on earth, one is on a spaceship, and both clocks seem to be working normally. However, the person on earth sees the spaceship differently: the light is moving both up and down and to the side, uniform with the ship. So for the space traveler, light travels at 300,000,000 m/s but only has to travel up and down. To the Earthbound observer, light travels at 300,000,000 m/s, but must travel a longer, diagonal distance. Then, for the Earthbound observer, the spacecraft clock takes longer to “tick”. This effect is called time dilation.

Al-Khalili then helps us visualize how this apparent paradox is resolved:

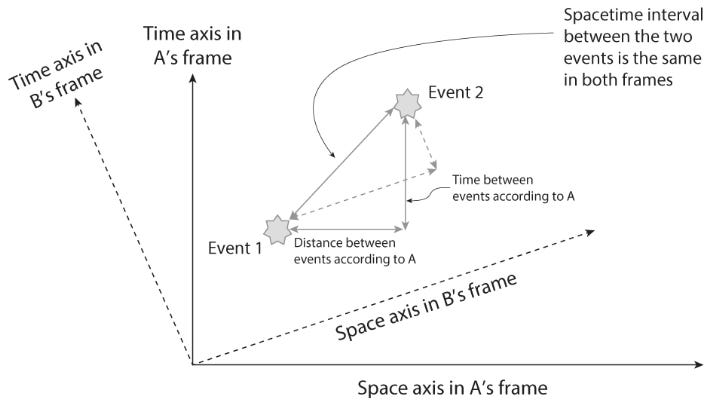
The special theory of relativity resolves this counterintuitive situation beautifully by combining time and space in order to retrieve something that we can all agree on. Imagine the whole of space is contained within a vast rectangular three-dimensional box. To define an event taking place within the box we assign to it x, y, and z coordinates (indicating its position relative to the three axes of the box) along with a value for time (when the event took place). Common sense would tell us that the time value is quite different from the three numbers defining the event’s location in space. But what if we could add a time axis to the three of space? It would need to be in a ‘direction’ that is at right angles to each of the three spatial axes, which is impossible for us to visualise. This would result in a combined four-dimensional volume of space-plus-time. An obvious simplification to help us with this visualisation is to sacrifice one of the dimensions of space and collapse our 3-D volume onto a two-dimensional surface, leaving the freed-up third dimension to use as the time axis. Now, think of this static block of space and time as a giant loaf of sliced bread, where the time axis lies along the length of the loaf. Each slice of bread is a snapshot of the whole of space at a single moment, while successive slices correspond to successive times. This is known in physics as the block universe model. While it is only three-dimensional (two of space and one of time), we must not forget that it really represents a four-dimensional construct: 4-D spacetime. Mathematically, we don’t have a problem dealing with four dimensions; it’s just picturing them that is not possible. Perceiving 4-D spacetime from the outside, we would experience the totality of existence, not only of all space, but of all times: past, present, and future, coexisting and frozen. It is an impossible viewpoint, an omniscient one, because in reality we are always trapped within the block universe and we experience the passage of time as a steady crawl along the time axis, moving smoothly from one slice of the loaf to the next, like frames in a movie stacked alongside each other instead of end to end on a reel. The reason the concept of the block universe is so useful is because it allows us to understand our different perspectives according to relativity theory. Two observers moving at high speed relative to each other might each record two events— say, flashes of light— but they will not agree on how far apart those flashes are or the time interval between them. This is the price we must pay if we are to all see light moving at the same speed. Viewed within the four dimensions of the block universe, spatial distances and time intervals can be combined, so the separation between any two events, called the spacetime interval, will be the same for all observers. Their disagreement about distances and times, if treated separately, turns out to be nothing more than different perspectives in spacetime. You and I can look at a cube from different angles so that what I see as its depth (the distance measured along my line of sight) will not appear the same to you if you see it face on. It depends on the angle at which we are looking at it. But we can nevertheless agree that it is a cube of equal- length sides, and that any differences are just down to our different perspectives. The same is happening in the 4-D block universe. We will always agree on spacetime intervals between events.

FIGURE 1. Events in spacetime—two observers, A and B, moving at high speed relative to each other, both see two events (flashes of light), which are separated in both space and time. They will not agree on the distance between the events, or on the time duration between them. This is because their space and time axes are different. But in 4-D spacetime (here two dimensions of space are ignored for simplicity) the (spacetime) interval between the two events in both frames is the same: the two right-angled triangles have the same hypotenuse even though each has a different space distance and time distance.

As Al-Khalili summarizes:

Einstein’s relativity teaches us that we must view things within 4-D spacetime, in which both spatial and temporal distances become just a matter of perspective. No observer has the right to claim that their perspective of space and time is more correct than any other, because we will all agree once space and time are combined. Individual perspectives of space and time separately are relative, but combined spacetime is absolute.

In the next essay in this series, we’ll continue to explore the modern understanding of space and time.

Links to other essays in this series: Part 1; Part 2; Part 3; Part 4; Part 5; Part 6.