Math’s Path – Part 3
Preventing the spread of disease; and preventing the spread of panic caused by poor estimations of risk.
As mentioned in previous essays in this series, while some schools were closed during COVID pandemic, kids suffered large learning losses, especially in math -- even as math was helping to stop COVID’s spread, and will help stop the spread of future illnesses as long as there are people proficient in math to do it. And learning losses are continuing as some school districts that are sticking with old COVID models of risk-reduction – even as math is dispelling the misunderstandings of risk on which those old policies are based.
Regarding math’s (and calculus’) vital importance in slowing the spread of disease, as Michael Brooks writes in The Art of More: How Mathematics Created Civilization:
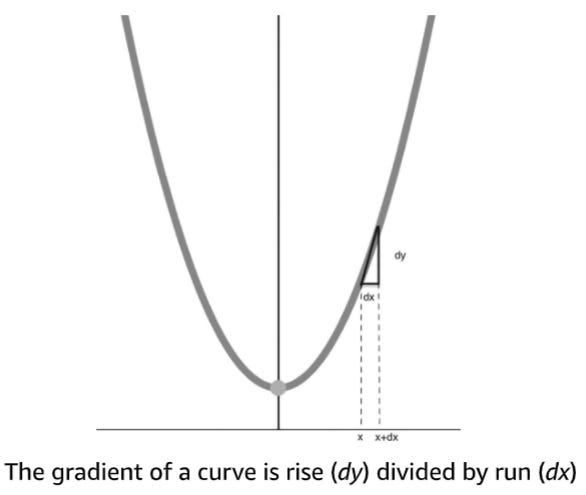
[L]et’s start with one practical application: finding the gradient, or slope, of a curve that is associated with the way a fatal infection proceeds in the human body. This use of calculus, it turned out, was instrumental in protecting us from the worst ravages of the human immunodeficiency virus (HIV) … It’s easy to forget just how bad things looked when HIV was at its most dangerous. After the first cases were reported in 1981, HIV quickly became the scourge of human populations across the globe. By 2007, HIV/AIDS had killed more than half a million Americans, and the US was refusing to admit any HIV-positive person into the country … Today, just over a decade later, HIV infection is no longer a death sentence. In fact, people with HIV live relatively normal lives. What happened? Calculus … The process generally starts with the algebraic equation for the curve. The slope is calculated by finding the ‘rise over run’: the vertical change in y (dy is used to signify change in y) that occurs over a horizontal change in x (dx, the change in x). The slope is then defined as the rise divided by the run: dy/dx. This is sometimes known as the ‘derivative’ of the equation that describes the curve. The derivative is easy to find when dealing with straight lines. But what if we are dealing with a curve like the one below?
[E]ssentially, it all boils down to finding the slope at a particular point … And that’s what Perelson did with his differential equations, which presented the rate of change of viral concentration of HIV, among other things, as the slope of a curve … The full analysis showed researchers that there were different phases of the infection that could all be modelled mathematically … [T]ogether they used calculus to prove that it would take a combination of three ‘antiretroviral’ drugs to essentially rid the body of HIV. That attack was ‘triple therapy’: a cocktail of three antiretroviral drugs that has turned HIV infection from a death sentence to a manageable problem.
Back in 1760, Daniel Bernoulli wrote “I simply wish that, in a matter which so closely concerns the wellbeing of the human race, no decision shall be made without all the knowledge which a little analysis and calculation can provide.” He was writing that calculus be applied to the question of whether it was worth vaccinating a population against smallpox. As Brooks writes:
His answer was an emphatic yes — and he had the data to prove it. According to Bernoulli’s calculations, 75 per cent of the 18th-century human population had been infected with smallpox. The disease was responsible for 10 per cent of all deaths; in London alone the number of smallpox fatalities reached 15,000 in some years. Adults were, by and large, immune; if they had survived, it was because their bodies had manufactured antibodies to the disease. But children were vulnerable. So, should they be given the new vaccinations? Well, said Bernoulli, I have equations for that. His first equation calculated the number of people who had never had smallpox, which was a fraction of the current population. His second equation forecast the annual number of infections and deaths due to smallpox, and the number of lives saved if smallpox were eradicated. Here is some of the original text: “the number of those who have not had smallpox at this age = s…the element -ds is equal to the number who catch smallpox in the period dx, and according to our hypotheses this number is sdx/n; for if, in the space of a year, 1 out of n catches smallpox, it follows that in a period dx there would be sdx/n who would catch the disease out of s persons …” In his analysis we see that familiar notation of dx and ds — all due to Leibniz [who, along with independently discovering calculus, came up with that notational system] — and, later, talk of integrals and differentials. His conclusion was that the numbers were clear: France should vaccinate. It was the first attempt to use mathematics to influence public health policy, and it could not have been done without calculus.
Today, COVID, unlike smallpox, has disproportionately harmed the elderly, not the young, and the risks of dying of COVID for all are being dramatically reduced by vaccination. As the United Press International reported:
Children age 10 and younger develop a more robust immune response to the coronavirus than other age groups, a study published Monday by JAMA Network Open found. Blood of younger children tested for antibodies to the virus had evidence of more than twice as many cells created by the immune system to fight off infections than adolescents and young adults, the data showed.
Generally, the risk of death from COVID-19 was about 3.5 times that of the seasonal flu, and that risk for most people was quite low. As further explained in the Wall Street Journal in 2020:
If you’re an average American living outside New York City, the epidemic was a period with barely noticeable increased risk. Your chance of being an extra fatality was about 1 in 5,000, somewhat higher than your chance of dying in an auto accident in a year. And if you were under 50 with no serious health conditions, your risk was in the ballpark of 1 in 50,000, similar to your risk of dying in a fire. In New York, those odds were approximately 1 in 300 and 1 in 3,000, respectively. “Nothing in life is to be feared, it is only to be understood,” Marie Curie observed. “Now is the time to understand more, so that we may fear less.” Covid-19 is a complex and fearsome challenge, but a little arithmetic can offer a lot of understanding.
And now that vaccines are freely available, new CDC research shows
that adults who are fully vaccinated against COVID-19 rarely die from the disease … Using data from 465 centers in a large US healthcare database, researchers analyzed the frequency of and risk factors for severe COVID-19 outcomes among adults who completed a primary vaccination series … Among 1,228,664 adults who completed primary vaccination during December 2020 and October 2021, 2246 (18.0 per 10,000 vaccinated persons) developed COVID-19 and 189 (1.5 per 10,000) had a severe outcome, including 36 who had a COVID-19–related death (0.3 deaths per 10,000).
Regarding children, as reported in New York magazine:
Elissa Schechter-Perkins, the director of Emergency Medicine Infectious Disease Management at Boston Medical Center, told me … “COVID, of course, is also a disease that tends to have much milder effects on children. We know that the risk to kids from COVID is vanishingly low. Yes, we’re seeing it, but it’s rare.” Out of more than 600,000 American deaths attributed to COVID-19 [at the time], 361 were for kids and adolescents under age 18. In the much-shorter 2018-2019 flu season, there were 477 pediatric deaths. “We didn’t have mask mandates then,” Schecter-Perkins noted. And “now we’re in a post-vaxx world where adults have had the opportunity to protect themselves, and vaccines prevent severe COVID.”
Dr. Anthony Fauci noted back in December, 2020, “The spread among children and from children is not really very big at all.”
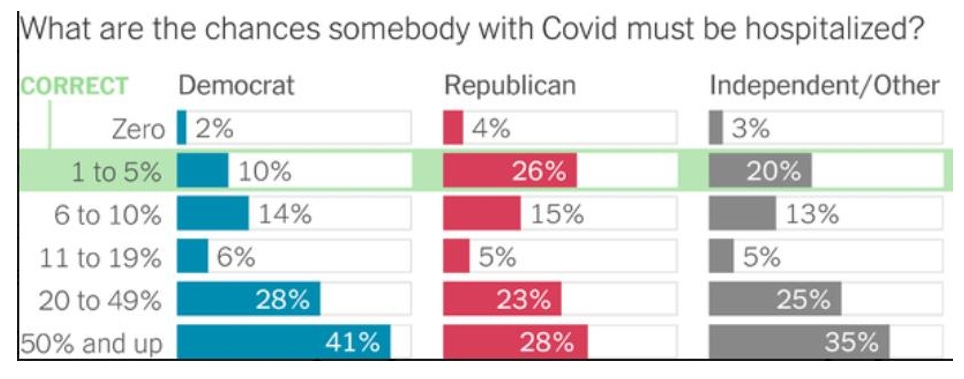
But risk for many has a strong emotional component, and with it comes some stark partisan differences in people’s threshold of risk aversion. As the New York Times reported, based on a survey of 35,000 Americans by Gallup and Franklin Templeton:
Democrats … are more likely to exaggerate the severity of Covid. When asked how often Covid patients had to be hospitalized, a very large share of Democratic voters said that at least 20 percent did. The actual hospitalization rate is between 1 percent and 5 percent. Democrats are also more likely to exaggerate Covid’s toll on young people and to believe that children account for a meaningful share of deaths. In reality, Americans under 18 account for only 0.04 percent of Covid deaths … The states with the highest share of closed schools are all blue states: California, Oregon, Maryland, New Mexico, Hawaii, Nevada, Massachusetts and New Jersey. “I think in many ways it’s based on the fact that these voters are misinformed about the risks to young people and they’re misinformed about the risks generally,” [Jonathan] Rothwell [Gallup’s principal economist] said.
And a May-June, 2020 survey conducted by the American Enterprise Institute found that Republicans reported much less risk aversion than Democrats regarding COVID-related risks:
There are massive partisan differences in feelings of comfort that span nearly every activity type. Two-thirds (67 percent) of Republicans say they would feel at least somewhat comfortable going to a polling place to vote compared to 31 percent of Democrats. A majority (57 percent) of Republicans say they would feel comfortable eating out at a restaurant, while only 21 percent of Democrats say the same. Republicans are more than twice as likely as Democrats are to express comfort in going to get a haircut (63 percent vs. 27 percent).
Does this partisan division in attitudes toward risk go far back in history, or is it a much more recent phenomenon? We’ll explore that question and others in the next essay.
Links to all essays in this series: Part 1; Part 2; Part 3; Part 4