Math’s Path – Part 1
Why math is so important.
We’ve just finished a series of essays on tax policy and, interestingly, when early governments first started to deal with the collection of taxes, it spurred developments in the field of math -- particularly geometry, which was used to calculate the area of fields and land for tax purposes. So let’s get a bigger picture and explore the vastly significant role math has played generally in civilizational progress.
This subject is particularly important now, as many students face math learning deficits. I wrote earlier about how masking and distancing policies at schools were hindering their ability to compete in a future workforce that evidence shows will rely heavily on math and analytical reasoning, as well as social, skills.
School closings have made the situation even worse, especially for kids in lower-income homes. As researchers including those from Yale and the University of Pennsylvania recently concluded:
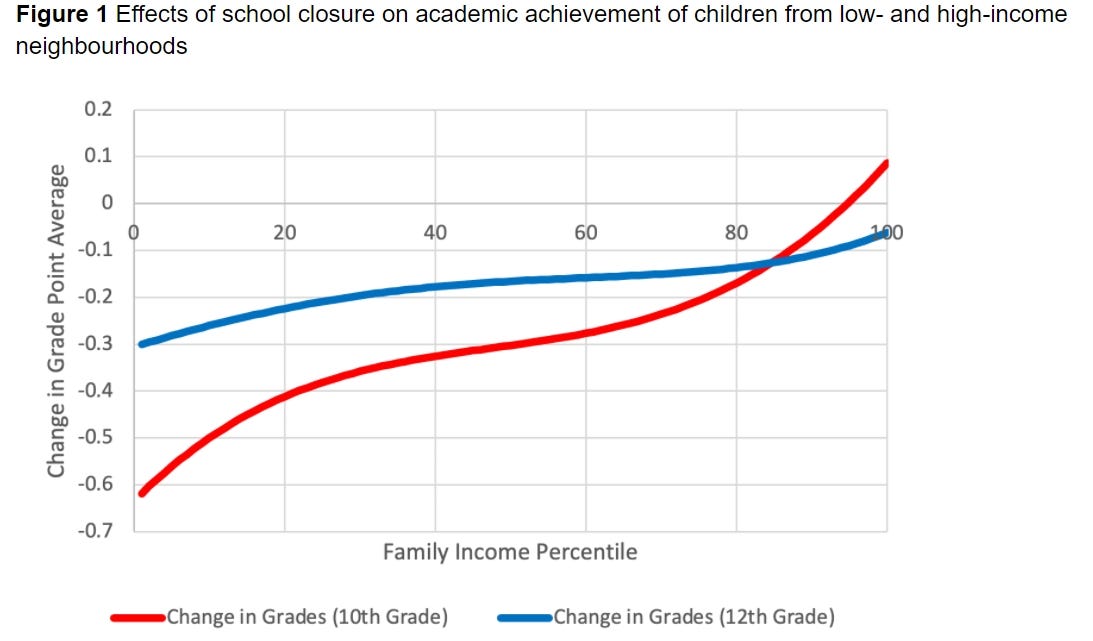
Our model predicts large learning losses for children from low-income families. The grades of children living in the poorest neighbourhoods decline, on average, by half a point on the 4-point GPA scale (see Figure 1). This loss for disadvantaged children is comparable to a change from a straight-B report card to getting a C in half of the subjects.
The researchers continue:
And the problem probably goes beyond high school: “Four years down the road, the school closure causes an average 25% reduction of labor earnings for the poorest children when these [kids] enter the labor market. This implies that the future society will be more unequal and have less social mobility.”
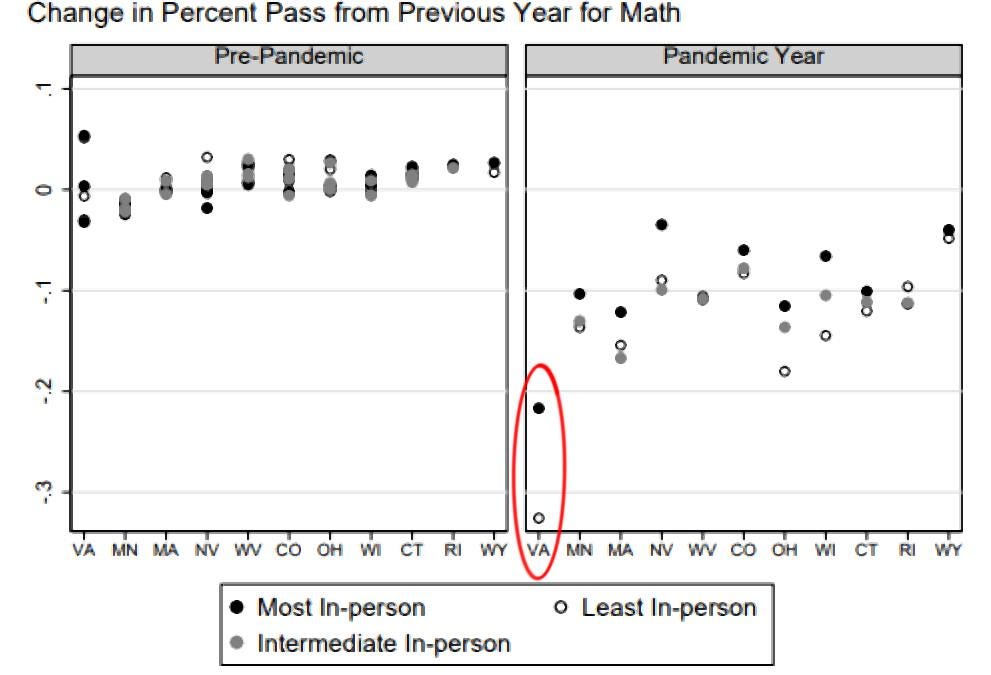
In Virginia, where I live, learning losses in math have been particularly dramatic. As other researchers point out, of the states they studied, Virginia had one of the highest shares of school district-time spent in fully virtual learning, and the largest losses in math learning, registering a 31.9 percentage point decline in performance on the standardized math test. (Virginia was also the only state studied that didn’t release data on standardized math test participation rates, and if we infer that the poorest kids were most likely to miss the test, it’s likely that math scores would have been even lower if there had been greater participation.)
So, some might say, who needs math anymore? We have calculators. True. But what else will we be missing as a society if the pool of students who can grasp higher-level math grows smaller and smaller? To get a sense of that, we need to look back at where math has gotten us as a civilization so far, and to do that, I’ll refer to Michael Brooks’ excellent book The Art of More: How Mathematics Created Civilization.
Adding and subtracting is essential to balancing ledgers, of course, which is essential to determining the success of a business, which is based on whether or not it’s able to make money by selling something people want at a cost they can afford. Without this innovation of “double-entry bookkeeping,” free markets and our resulting increased living standards would never have materialized, and they can’t continue without those who can do the math. As Brooks explains:
As well as facilitating trade, double-entry bookkeeping changed the way businesses grew and operated. The double-entry system is centered on the accounting equation Assets = Liabilities + Owner’s Equity. In other words, the health of the business is the sum of its debts and its current holdings, which are all accounted after every transaction. This allows anyone associated with a business to know at a glance what it is worth. So if you were considering whether to loan money or goods to a company, you could see exactly what you were getting involved with in terms of debts, operating costs, assets, loans, and net worth. No more taking the owner’s word for it, or trusting the family name … It is hard to comprehend just how revolutionary this would have been when the system first came into widespread use. There was no longer any need to keep things in the family and stick to one line of business; you could build a firm and treat it as you would disposable capital. If you fancied starting another business alongside your first, the books could prove your business acumen, and even be used as security against a loan.
More advanced math (trigonometry) allowed businesses that could prove their worth this way to carry their goods around the world:
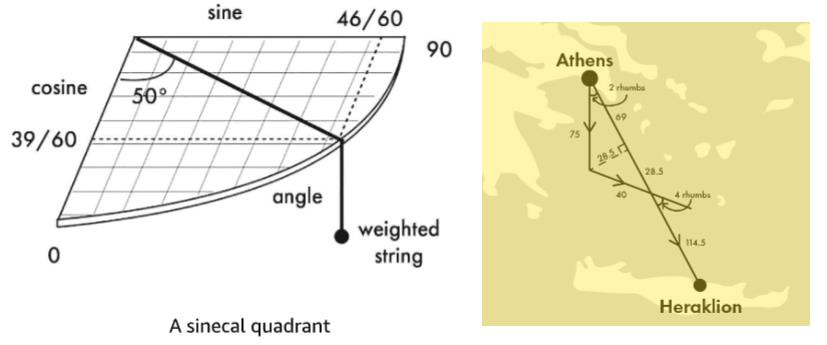
Sines, like cosines and tangents, are just ratios — comparisons, if you like — of the lengths of a triangle’s sides … “Navigation is nothing more than a right triangle,” said the French mariner Guillaume Denys in 1683. He is referring to what we call a right-angled triangle: the properties of this shape, he says, are all a sailor needs to understand. It was a truth that had been established for hundreds of years … [W]hen ships went off course during a journey, whether it was because of unfavourable winds, an island in the way, or because they were waylaid by pirates, the crew would use the mathematics of triangles — trigonometry — to set them back on course. That’s why they carried tables of sines and cosines, or an instrument that could calculate them, such as the sinecal quadrant.
Sailors would estimate their ship’s speed by throwing wood overboard and counting the time it took for it to pass a known length of the hull. They could then calculate their distance traveled over time, then use that information to make their path part of a triangle whose other sides they could then measure, and correct their course when necessary. As Brooks writes, “Sailors might have a reputation for ignorance, illiteracy and brutish behaviour, but many of them were accomplished mathematicians nonetheless.”
Using flat triangles to measure worked fine for short distances. But the Earth is a sphere, with always curving sides, and over long distances any imagined navigational triangles would have to curve, too:
The complication introduced by the spherical nature of the Earth’s surface is the central problem of map-making … For many thousands of years, map-makers have sought “projections” of the spherical surface that minimise just how misleading their map might be. A projection takes the latitude and longitude and performs a mathematical operation on them so that, when drawn on a flat plane, the angles and distances between all the various points make sense. The maths involved is a combination of the geometry of spheres and trigonometry … Ptolemy [an ancient Greek mathematician] published this map in his book Geographia. This is a projection with latitude and longitude lines, which was revolutionary at the time.
Today we use even more sophisticated map projections that allow us to use GPS systems to locate ourselves precisely, anywhere on Earth:
[T]he mathematical tricks required to achieve this eluded NASA’s best scientists for decades. The man who eventually worked it out was the unsung hero John Parr Snyder … In 1972, NASA launched Landsat-1, the first satellite built to study the Earth’s geography. To insiders, it was clear that the satellite could also provide an entirely new kind of world map, and two years later the cartographic coordinator for the United States Geological Survey (USGS) published a paper describing a suitable mathematical projection. Alden Colvocoresses — Colvo to his friends — imagined a map that would account for the movement of the satellite’s scanner, the satellite’s orbit, the rotation of the Earth, and the way the axis of that rotation evolves in a 26,000-year cycle thanks to Earth’s “precession.” … But no one at NASA or the USGS knew how to do the geometric analysis required to actually construct the projection … [Snyder] spent five months of his evenings and weekends solving it, using his spare bedroom as a study and nothing more technical than a Texas Instruments TI-56 programmable pocket calculator … Snyder’s paper laying out the ideas behind it involves a complex array of sines, cosines, and tangents. Thousands of years after we first discovered its properties, we are still harnessing the power of the triangle.
The mapping allowed by this math is essential to military operations, weather forecasting, Google Maps, and every other digital mapping technology. But how to transmit those maps to the people who need to see them? Through waves, whether they occur by sound, electromagnetism, or any other medium. And when you measure waves, you do so by tracking the movement of things that go around in a circular pattern, which required the discovery of π, which itself was discovered through the use of triangles:
[T]he circumference of a circle is π times the circle’s diameter … Archimedes found his approximation of it by first drawing a multi-sided shape (a polygon) inside a circle. He then split that shape up into triangles whose base is one of the polygon’s sides (the other two sides being radii of the circle). By calculating the area of each of these “isosceles” triangles, you can work out the area covered by the polygon. The more triangles you draw, the closer the polygon comes to covering the area of the circle, and the more accurate your value of π … By 240 B.C., when Archimedes was looking at the properties of wheels, he had pegged π at somewhere between 3.140 and 3.142 (by using a 96-sided polygon).
What might we all be losing when kids lose their “math sense” of measurable space? As Brooks writes of these math pioneers:
Their achievements are a testimony to the power of the human brain — something we might well forget in the modern age where so much is done for us. I can open a CAD program if I want to design a geometrical structure. I can open an app on my phone if I want to know where on Earth I am, or how to get to a specific point. Airline pilots are still trained in working out rhumb lines and loxodromes in case their GPS fails, but the rest of us have no need of the ancient ways. I can’t help feeling that, in some ways, we might be the poorer for it. Some researchers argue, for instance, that our disconnection from geometry stymies our creativity. Our brains now lack a dimension of capability that used to exist in students who actually used geometrical thinking, they say … [L]earning to handle algebra increased your ability to think in abstract terms, and to pay attention to something your brain would rather not think about. Millennia of experience and some interesting modern research has taught us that (as with geometry) dealing with abstract varying quantities and the numerical relationships between them actually makes our minds work better. Algebra makes you creative, productive, and tenacious, a lateral thinker capable of pushing through to the end of a line of thought.
The routes by which goods are delivered to us are determined by algebra:
FedEx and UPS are classic logistics operations … Human realization has been built on solving logistics issues, whether it was the ancient Egyptians’ construction of the pyramids, Napoleon’s realization that an army marches on its stomach, or the modern-day problem of ensuring airline pilots, Amazon deliveries, and packets of information traversing the worldwide web are exactly where they need to be at any given moment. All of these challenges involve solving a series of puzzles that mathematicians call algebra … Processing lots of variables simultaneously, and finding out the relationship between them all so you can optimize one particular outcome of their actions, is something we do well now. As well as Google searches, it also powers airlines: flight schedules, fleet plans, aircraft routes, crew pairings, gate assignments, maintenance schedules, food service plans, training schedules, and baggage handling procedures are all optimization problems solved using linear algebra.
An even higher form of algebra called abstract algebra is used in particle physics, and to discover new particles and the forces that work on them:
You might swap a particle for its antiparticle, for example. If you see no difference in how their interactions happen, that’s a symmetry. A good example of this is when you change the charge on two electrons to its opposite. Two positrons repel each other in exactly the same way as two electrons do. That’s charge symmetry. Symmetries are at the heart of our understanding of the physical world, because many of the processes of physics can be expressed in terms of reflections, rotations, or simple swaps. Those symmetries might be in space, or in time, as well as in physical properties like electrical charge. There is a deep connection between symmetry and the conservation laws that say certain properties of a physical system cannot simply disappear. Take the law of conservation of energy, for example. You might remember from your physics lessons at school that you can convert energy from one form to another — from kinetic to potential, say, by rolling a boulder to the top of a hill — but that energy won’t ever disappear from the universe … [A]bstract algebra means that we can use her equations to look for new laws, particles, and forces of physics. When symmetry is broken, there is always a reason, and usually it’s because of a force. In fact, this has typically been how physicists discover the existence of an as yet unknown force of nature.
In the next essay, we’ll explore the math that’s been called the most influential innovation in history, much bigger than the wheel, and the amazing story behind the discovery of calculus.
Links to all essays in this series: Part 1; Part 2; Part 3; Part 4