Machine Learning, ChatGPT, and Bayes’s Theorem – Part 5

A summary and some more practical applications of Bayes’s theorem today.

In this essay, we’ll use Tom Chivers’ book Everything Is Predictable: How Bayesian Statistics Explain Our World to help summarize what we’ve explored so far in this essay series, and to describe some of AI machine learning’s practical applications today.

As Chivers writes, regarding Bayes’ theorem, or Bayes’ rule:

As equations go, it is simple. It looks like this:

But equations aren’t secret codes or arcane magic. Each little symbol (I have to remind myself) denotes a simple action. It’s just a sort of shorthand.  In this case, Bayes’ theorem is about probability: about how likely something is, given the evidence we have. Specifically, it’s about a particular form of conditional probability. The vertical line | is shorthand for “in the event that” or “conditional on.” So P(A|B) is the probability of an event A happening, given that event B has happened. Here’s a simple example of conditional probability: say you wanted to know the probability of drawing a heart from a deck of cards. You know there are thirteen hearts in a standard fifty-two-card deck, so your probability—P(heart), if you like—is 13/52, or 1/4. Or, in probability notation, p = 0.25. But then you draw a card, and it’s a club. What’s your probability now? Well, there are still thirteen hearts in the deck, but only fifty-one cards in total. So your probability is now 13/51, or p ≈ 0.255. (The wavy equals sign means “approximately equal to.”) That’s the probability of drawing a heart given that you’ve previously drawn a club, P(heart|club).  Or: What’s the probability that it will rain on a given day in London? Probably about 0.4: there are around 150 rainy days a year in London. But you look out the window and you see that the clouds are dark and heavy. What’s the probability now? I don’t know exactly, but higher: the probability of rain given that it’s cloudy is higher. Bayes’ theorem is the same idea, but taken a bit further. In natural language it means: the probability of event A, given event B, equals the probability of B given A, times the probability of A on its own, divided by the probability of B on its own.

Regarding AI, Chivers writes:

Artificial intelligence is essentially applied Bayes. It is, at its most basic level, trying to predict things. A simple image classifier that looks at pictures and says they’re of a cat or a dog is just “predicting” what a human would say, based on its training data and the information in the picture. DALL-E 2, GPT-4, Midjourney, and all the other extraordinary AIs that are wowing people as I write, the things that can hold conversations with you or create astonishing images from simple text prompts, are just predicting what human writers and artists would make from a prompt, based on their training data. And the way they do it is Bayesian. Our brains are Bayesian. That’s why we are vulnerable to optical illusions, why psychedelic drugs make us hallucinate, and how our minds and consciousnesses work at all. Once you start looking at the world through a Bayesian lens, you do start seeing Bayes’ theorem everywhere.

Chivers then begins to explain the important concept of “priors” in Bayesian reasoning:

[T]he important thing is that you have to start with a prior probability, and use Bayes’ theorem. If you don’t, you end up in some strange places … There’s something wonderful about how counterintuitive the theorem is. What do you mean, a test being 99 percent accurate isn’t the same as a 99 percent chance that it’s right? What mad language are you talking? If you follow the really-not-that-difficult reasoning, it becomes clear, but—for me, at least—it never quite loses its uncanny, otherworldly feeling.

Regarding some real-world applications of Bayesian reasoning, Chivers writes:

In law, there’s a thing called the prosecutor’s fallacy, which is quite literally just not thinking like a Bayesian. Imagine you do a DNA test on a crime scene. You find a sample on the handle of the murder weapon that matches the DNA of someone in your database. The DNA match is quite precise—you’d only expect to see a match that close about one time in every 3 million. So does that mean that there’s only a one-in-3-million chance that your suspect is innocent? By now, hopefully, you’ll have realized that’s not the case. What you need to know is your prior probability. Is there any particular reason to think this person is the right one, or is your database just a random selection of people from the British population? If so, then your prior probability that the person you’re accusing is the criminal is one in about 65 million: there are 65 million Britons and only one person who committed this particular crime. If you DNA-tested every Briton, you’d get about twenty DNA matches, just by chance, plus the perpetrator. So the probability that you’ve got the right suspect is about 5 percent, give or take. But if you had narrowed it down to just ten suspects beforehand—say that you’re Hercule Poirot and you know it’s one of ten people trapped in a country mansion by a snowstorm—then it’s very different. Your prior probability is 10 percent. If one of those ten people match the DNA, then your probability of a false positive is about one in three hundred thousand … During the trial of O. J. Simpson, the former American football star, for the murder of his wife, Nicole Brown Simpson, the prosecution showed that Simpson had been physically abusive. The defense argued that “an infinitesimal percentage—certainly fewer than 1 in 2,500—of men who slap or beat their wives go on to murder them” in a given year. But that was making the opposite mistake to the prosecutor’s fallacy. The annual probability that a man who beats his wife will murder her might be “only” one in twenty-five hundred. But that’s not what we’re asking. We’re asking if a man beats his wife, and given that the wife has been murdered, what’s the probability it was by her husband? We can now do the Bayesian maths. If we take 100,000 domestic abuse victims, then, presumably, in a given year, 99,955 are not murdered. But of the remaining 45, 40 are murdered by their husbands. The defense had made the inverse of the prosecutor’s fallacy: they had used just the prior probability, and ignored the new information coming in.

Chivers continues:

Bayes’ theorem … can tell us more profound things too. The word “inverse” … is key. Often, statistics and probability will tell you how likely it is that you’ll see some result by chance. If my dice are fair, I’ll see three sixes at the same time 1 time in every 216. If I was never at the crime scene, my DNA should match the sample 1 time in every 3 million. Often, though, that’s not what we want to know. If we’re worried that the person we’re playing craps with is a cheat, we might want to know “If he rolls three sixes, what are the chances that his dice are fair?” If someone’s DNA matches the sample at the crime scene, we might want to know what the chances are that it’s a fluke. And that is the exact opposite question. For quite a long time, the history of probability was about asking the first question. But after the Reverend Thomas Baye … started asking the second one, in the eighteenth century, it became known as inverse probability … [Bayesian reasoning] affects everything. How likely is a scientific hypothesis to be true, given the result of some study? Well, I can tell you the probability that you’d see the results we’ve seen if it weren’t true, but that’s not the same thing. To estimate how likely it is—and a growing number of scientists argue that that’s exactly what we want statistics to be doing—we need Bayes, and we need prior probabilities. More than that, all decision-making under uncertainty is Bayesian—or to put it more accurately, Bayes’ theorem represents ideal decision-making, and the extent to which an agent is obeying Bayes is the extent to which it’s making good decisions.

Returning to the all-important concept of “priors,” Chivers writes:

The thing with Bayesianism is that you have to have priors. Throughout its history, that’s been a sticking point—Where can you get them from? How much of a problem is it that they seem to be subjective? … In deciding between possible hypotheses, one way to establish your priors is to look at which is more complex. Things that are more complex are less likely to arise by chance—so all else being equal, presented with two possible explanations, one simple and one complex, your priors should favor the simple one. There’s a name for that—Occam’s razor. It’s named after a fourteenth-century Franciscan monk called William of Ockham, who lived in Ockham, Surrey.II But how do we decide what the simplest explanation is? When we look at the world, often the explanations for things seem very complicated indeed. But decision theorists have a more formal definition of simplicity. The fact that something can be described in a short English sentence doesn’t necessarily tell us very much about how simple that thing is—I can say “the human brain” in four syllables, but the brain itself is the most complex thing in the universe. Instead, decision theorists use something called minimum message length. (I could also describe it as “Solomonoff induction” or “Kolmogorov complexity.” The three are subtly different, but at heart they’re equivalent.) What minimum message length asks is: What is the shortest computer program I could write that would describe a given output? … The trade-off is between the complexity of the algorithm and how confidently it would predict the output … So in choosing between two or more hypotheses, you should (in theory) be able to look at which is the more complex, and—all else being equal—assign higher prior probability to the one that would be simpler to write as a computer program. There are other ways of producing priors, but minimizing complexity like this is a key one.

To illustrate:

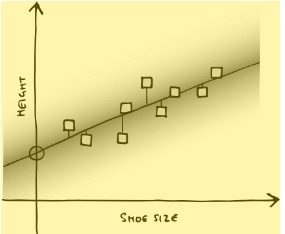
Say you have some hypothesis, like “vaccines cause autism” or “man- made climate change is real,” and you assign it some given prior probability. You take two people, one who thinks the hypothesis is likely, and the other who thinks it’s not. Then you give them some piece of evidence, like an article on the BBC News website saying, “These scientific studies show that autism rates didn’t spike after the introduction of the MMR vaccine,” or “these scientific studies show that the world is getting warmer and it roughly tracks atmospheric carbon dioxide concentrations.” Just as with the telepathy example, if the only possible explanation for the evidence is that the hypothesis is right (or wrong), then that evidence should help the two people’s opinions converge. But there’s an alternative hypothesis: that the source is untrustworthy. If one person strongly believes that MMR causes autism or that climate change isn’t real, then the evidence will not bring them closer to the other person’s beliefs, but will instead push them into saying, “This is why the BBC can’t be trusted.” (Or, if the BBC provides links to the scientific papers, “This is why the scientific establishment can’t be trusted.”) And, disturbingly, in many cases, that would be the rational thing to do … At its heart, artificial intelligence is just a program that tries to predict uncertain things. By this point, you won’t be surprised when I say that it is fundamentally Bayesian. Artificial Intelligence: A Modern Approach, the standard textbook for undergraduate AI degrees, even has a picture of Thomas Bayes on the front cover, and says, “Bayes’ rule underlies most modern approaches to uncertain reasoning in AI systems.” … Let’s simplify the situation even further and look at it as a graph. This even simpler AI is just looking at where a bunch of blobs are on a graph and trying to find the line of best fit through them. This isn’t something you need a powerful AI for: it’s just a linear regression, statistics that Francis Galton would have been entirely comfortable with. But it’s the same principle. Let’s take a chart of people’s shoe size versus their height. You take a large, random sample of people, measure their height and their feet, and plot them on a graph—foot size along the x-axis, height up the y-axis. As you’d expect, on average, taller people have larger feet, but there’s some variation. So the dots tend to line up from bottom left to top right. What your AI wants to do is draw a line through them. You could draw the line by eye, but there’s an established system called the line of least squares. Draw a line on the graph and measure the vertical distance from the line to each dot. That distance is the error, or the loss. For each dot, square the error—that is, multiply it by itself, so that all the numbers are positive. (A negative number squared is positive.) Then add the squared error for all your dots together. That figure is the sum of squared error. What you want to find is the line with the lowest squared error: the one that has the smallest average distance to all the dots.

Those dots are your AI’s training data. And, of course, it’s a Bayesian process. It starts out with a flat line, a flat prior. Then as you add dots—your data—the line moves, to give you the posterior distribution, which becomes the prior for the next bit of data. But now you want to use it to make predictions. Say you give it someone’s shoe size, and you ask it to guess that person’s height. All it needs to do is go along the x-axis to the relevant bit—size 11, say—and then go up on the graph to where the line of least squares is. That’s its best guess for the person’s height. How confident it is depends on how much training data it has and the variance in that data—if it’s very spread out, then the guess will be less confident. This is, roughly, what real AIs do. They do much more complicated versions, with hundreds or thousands of parameters instead of just “shoe size” and “height,” but the basic idea is the same. They have some training data, and they use it to predict the value of some parameter or parameters, given some other parameter. Often, an AI is trained just once, and the test data doesn’t change its priors. But that doesn’t need to be the case. It could easily be that the AI continues to update on each piece of training data. The shape of the line each time is its prior, the new data point is the likelihood, and together they make a new posterior probability. The farther each dot is from the line, compared to where it was predicted to be, the more the model is “surprised” by it and updates its prediction for the next one. Equally, your AI could, assuming it is sophisticated enough, simply draw a wibbly-wobbly line that goes perfectly through the heart of every dot in the training data. That would give it a squared error of precisely zero. But it probably wouldn’t represent the real underlying cause of the data. When new data arrives, it’ll most likely be a long way away from the weird wibbly-wobbly line your AI has drawn, because it’s “overfitted” to the data. The question, therefore, is how much freedom the AI has to wobble the line around. That freedom is analogous to what in the last section we called “hyperparameters”—as well as the simple question of the best-fitting curve, there’s a higher-level question of how wobbly that curve should be. The AI’s prior beliefs about those parameters are its hyperpriors. And they often decide that, all else being equal, you choose the simpler of two lines. You trade off simplicity against fit. Just what we were saying in the section on Occam priors.

[W]hen ChatGPT writes a short story in the style of the King James Bible about a man getting a peanut butter sandwich trapped in his VCR, they’re doing something Bayesian. They are using their training data to produce prior probabilities, which they then use to predict future data.

While the physical structure of AI machine learning systems are vastly different from our human brains, our own brains also rely on Bayesian reasoning.  As Chivers explains:

There was a study released in 2023 that used an AI that had a similar architecture to an LLM like GPT, but was instead trained on the board game Othello, a Go-like game in which players take turns to place small black or white disks on an eight-by-eight board. All it saw was game notation from tens of thousands of games, tokens noting where each player placed their disks. The idea was to see whether the AI simply memorized a load of statistics about the game—noticing that “f5” is often followed by “d6” in the notation, for instance—or whether it built an internal representation of the board. That would be a “world model,” albeit only of the small, limited world to which the AI had access. They then looked to see if the AI would make original, legal moves that it had never seen before—by artificially restricting its training data, removing all games starting with one of the four possible moves, so that they knew that all games starting with that move would be novel to the AI. And yet it still made very few errors—only one of its moves in every five thousand was illegal. It was clearly not simply memorizing the statistical correlations. Then they used a technique called “probing” to look at the internal state of the AI at certain points, and see if they could use it to predict the board state of the game at that moment. They could, with considerable accuracy—which showed that the AI had created some sort of representation of the board. Then they changed those internal states manually, so that its model of the board would be different, and the AI made moves that would only be legal in those board states, implying that it was using that internal representation to make decisions … Othello-GPT uses the same basic architecture as ChatGPT and the other LLMs, so it’s reasonable to assume that these findings tell us something about all of them … [I]n quite a real sense, all humans are doing is “predicting” the world around us. But in order to do so, we build a sophisticated, rich model of that world, to help us make good predictions. The suggestion is not that ChatGPT, or Othello-GPT, understands the world in anything like the way that we do. But it does show that just predicting is more than just autocomplete. Prediction—which, remember, is an inherently Bayesian process—gets you a long way toward intelligence … People are also bad at explicitly working out how to incorporate prior probabilities and new evidence—at being conscious Bayesians, in other words. That’s true even of people who really ought to be doing better at it. A famous 1978 study asked sixty medics—twenty medical students, twenty junior doctors, and twenty more senior doctors—at Harvard Medical School the following question: “If a test to detect a disease whose prevalence is 1/1000 has a false-positive rate of 5%, what is the chance that a person found to have a positive result actually has the disease, assuming you know nothing about the person’s symptoms or signs?” As you’ll know from having read this far, it’s pretty easy to work out. I tend to do it by imagining a much larger group—say a million. Of the million, 1,000 will have the disease and 999,000 won’t. Of the 999,000, our test will return false positives on 49,950. So assuming it correctly identifies all 1,000 who do, anyone who has a positive test will have a slightly less than 2 percent chance of having the disease (1,000/ (49,950 + 1000) ≈ 0.02). This seems like something important for doctors to be able to work out. But the 1978 study found that only eleven of the sixty medics gave the right answer (and those eleven were evenly spread among the groups: the students did no worse than the senior doctors). Nearly half said 95 percent: that is, they failed to take base rates into account at all … Even with things like, say, vaccine hesitancy—if you have low trust in public health systems, then your prior will be to distrust vaccines, and you won’t update much on new evidence coming from public health experts. That is, given your priors, perfectly rational. If someone wanted to persuade you otherwise, they would do better to build your trust in public health systems, rather than to provide you with a list of public health experts saying that vaccines are safe … Bayesian reasoning requires you to use all the information at your disposal. You don’t just know that Monty opened a door: you know (or you have some reason to believe) his algorithm for opening that particular door. You know why he did it. And that information changes your beliefs, and therefore your estimate of the probability that the car is behind any particular door. But that feels weird to us. Just as it feels weird that you can get a positive result on a 95 percent accurate test and still only have a 2 percent chance of having the disease it tests for.

Chivers then describes what might be an even more counter-intuitive result:

This all gets much weirder (or it does for me) in the second example, the “Boy-Girl paradox,” created by the American science popularizer Martin Gardner in 1959. Imagine you meet a mathematician, and they tell you that they have two children. You ask if at least one of them is a boy. (It’s a strange question, but this problem is incredibly sensitive to tiny changes in wording, so I have to be careful.) The mathematician says, yes, at least one of their children is a boy. What’s the chance that they are the parent of two boys? It obviously should be fifty-fifty. The other one is a girl or a boy! It doesn’t matter what the one you know about is! But… it’s not. The chance is one-third again. As you may be able to tell, this drives me crazy. But it’s very much unavoidable. Just as Fermat and Pascal realized nearly four hundred years ago, what matters is the number of possible outcomes (assuming that all those outcomes are equally likely). There are four possible pairs of children that a parent of two might have: girl-girl, girl-boy, boy-girl, and boy-boy. They’re all, to a first approximation, equally probable. If you know that at least one of the children is a boy, but you don’t know which one, then you’ve ruled out one of those combinations—girl-girl. Girl-boy, boy-girl, and boy-boy all remain. You’ve already got one boy in the bank, as it were. So the other child is either a girl or a boy. The unknown child is twice as likely to be a girl as to be a boy. (Which I find weird because it’s like there’s some strange quantum effect where knowledge of one child affects the sex of the other.)

That concludes this essay series on machine learning, ChatGPT, and Bayes’s theorem.