Machine Learning, ChatGPT, and Bayes’s Theorem – Part 3
Bayes himself, his times, and his relevance today.
This continues an essay series on how the sort of AI that entails what’s become called “machine learning” works, using Anil Ananthaswamy’s book Why Machines Learn: The Elegant Math Behind Modern AI, and Tom Chivers’ book Everything Is Predictable: How Bayesian Statistics Explain Our World, to help explain things. This essay focuses on Thomas Bayes himself, his times, and his relevance today, using Chivers’ book, and also Sharon Bertsch McGrayne’s The Theory that Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy.
As Chivers writes:
Bayes was an eighteenth-century Presbyterian minister and a hobbyist mathematician. In his lifetime, he wrote a book about theology and another about Newton’s calculus. But what he is remembered for is his short work, “An Essay towards Solving a Problem in the Doctrine of Chances.”1 It was published posthumously, in the journal Philosophical Transactions, after his friend Richard Price found and edited some unfinished notes Bayes left behind … This book is about the deceptively simple idea that Bayes came up with, his theorem. It is, without exaggeration, perhaps the most important single equation in history.
McGrayne provides more historical context, starting with the influence the eighteenth-century Scottish philosopher David Hume had on Bayes. As McGrayne writes:
[David] Hume argued that certain objects are constantly associated with each other. But the fact that umbrellas and rain appear together does not mean that umbrellas cause rain. The fact that the sun has risen thousands of times does not guarantee that it will do so the next day. And, most important, the “design of the world” does not prove the existence of a creator, an ultimate cause. Because we can seldom be certain that a particular cause will have a particular effect, we must be content with finding only probable causes and probable effects. Hume’s essay was nonmathematical, but it had profound scientific implications. With Hume’s doubts about cause and effect swirling about, Bayes began to consider ways to treat the issue mathematically … Bayes decided that his goal was to learn the approximate probability of a future event he knew nothing about except its past, that is, the number of times it had occurred or failed to occur. To quantify the problem, he needed a number, and sometime between 1746 and 1749 he hit on an ingenious solution. As a starting point he would simply invent a number— he called it a guess— and refine it later as he gathered more information. Next, he devised a thought experiment, a 1700s version of a computer simulation. Stripping the problem to its basics, Bayes imagined a square table so level that a ball thrown on it would have the same chance of landing on one spot as on any other. As he envisioned it, a ball rolled randomly on the table could stop with equal probability anywhere. We can imagine him sitting with his back to the table so he cannot see anything on it. On a piece of paper he draws a square to represent the surface of the table. He begins by having an associate toss an imaginary cue ball onto the pretend tabletop. Because his back is turned, Bayes does not know where the cue ball has landed. Next, we picture him asking his colleague to throw a second ball onto the table and report whether it landed to the right or left of the cue ball. If to the left, Bayes realizes that the cue ball is more likely to sit toward the right side of the table. Again Bayes’ friend throws the ball and reports only whether it lands to the right or left of the cue ball. If to the right, Bayes realizes that the cue can’t be on the far right- hand edge of the table. What Bayes discovered is that, as more and more balls were thrown, each new piece of information made his imaginary cue ball wobble back and forth within a more limited area. As an extreme case, if all the subsequent tosses fell to the right of the first ball, Bayes would have to conclude that it probably sat on the far left- hand margin of his table. By contrast, if all the tosses landed to the left of the first ball, it probably sat on the far right. Eventually, given enough tosses of the ball, Bayes could narrow the range of places where the cue ball was apt to be. Bayes’ genius was to take the idea of narrowing down the range of positions for the cue ball and— based on this meager information— infer that it had landed somewhere between two bounds. This approach could not produce a right answer. Bayes could never know precisely where the cue ball landed, but he could tell with increasing confidence that it was most probably within a particular range. Using his knowledge of the present (the left and right positions of the tossed balls), Bayes had figured out how to say something about the past (the position of the first ball). He could even judge how confident he could be about his conclusion.
Hannah Fry and Matt Parker perform the very same experiment Bayes ran, in his own home, here:
The Royal Society produced this video on Bayes and his theorem here:
And the excellent 3Blue1Brown explains Bayes theorem this way (with much more attention to describing the math and the symbols used in the equation):
Back to McGrayne:
Conceptually, Bayes’ system was simple. We modify our opinions with objective information: Initial Beliefs (our guess where the cue ball landed) + Recent Objective Data (whether the most recent ball landed to the left or right of our original guess) = A New and Improved Belief. Eventually, names were assigned to each part of his method: Prior for the probability of the initial belief; Likelihood for the probability of other hypotheses with objective new data; and Posterior for the probability of the newly revised belief. Each time the system is recalculated, the posterior becomes the prior of the new iteration. It was an evolving system, which each new bit of information pushed closer and closer to certitude. In short: Prior times likelihood is proportional to the posterior.
McGrayne then describes the slow road to the recognition of Bayes’s insight:
Two especially popular targets for attack were Bayes’ guesswork and his suggested shortcut. First, Bayes guessed the likely value of his initial belief (the cue ball’s position, later known as the prior). In his own words, he decided to make “a guess whereabouts its probability is, and ... [then] see the chance that the guess is right.” Future critics would be horrified at the idea of using a mere hunch— a subjective belief— in objective and rigorous mathematics … Although Bayes’ idea was discussed in Royal Society circles, he himself seems not to have believed in it. Instead of sending it off to the Royal Society for publication, he buried it among his papers, where it sat for roughly a decade. Bayes’ discovery was still gathering dust when he died in 1761. At that point relatives asked Bayes’ young friend Richard Price to examine Bayes’ mathematical papers. Price, another Presbyterian minister and amateur mathematician, achieved fame later as an advocate of civil liberties and of the American and French revolutions. His admirers included the Continental Congress, which asked him to emigrate and manage its finances; Benjamin Franklin, who nominated him for the Royal Society; Thomas Jefferson, who asked him to write to Virginia’s youths about the evils of slavery; John Adams and the feminist Mary Wollstonecraft, who attended his church; the prison reformer John Howard, who was his best friend; and Joseph Priestley, the discoverer of oxygen, who said, “I question whether Dr. Price ever had a superior.” When Yale University conferred two honorary degrees in 1781, it gave one to George Washington and the other to Price. An English magazine thought Price would go down in American history beside Franklin, Washington, Lafayette, and Paine. Yet today Price is known primarily for the help he gave his friend Bayes. Sorting through Bayes’ papers, Price found “an imperfect solution of one of the most difficult problems in the doctrine of chances.” It was Bayes’ essay on the probability of causes, on moving from observations about the real world back to their most probable cause. But once Price decided Bayes’ essay was the answer to Hume’s attack on causation, he began preparing it for publication. Devoting “a good deal of labour” to it on and off for almost two years, he added missing references and citations and deleted extraneous background details in Bayes’ derivations … Given the revered status of [Bayes’s’] work today, it is also important to recognize what Bayes did not do. He did not produce the modern version of Bayes’ rule. He did not even employ an algebraic equation; he used Newton’s old- fashioned geometric notation to calculate and add areas. Nor did he develop his theorem into a powerful mathematical method.
As Chivers writes:
What Bayes showed in his paper “An Essay towards Solving a Problem in the Doctrine of Chances” was that in order to make inferential probability work—which means, remember, asking, “What are the chances that my hypothesis is true, given the data?” rather than “What are the chances that I would see this data, given my hypothesis?”—you must take into account how likely you thought the hypothesis was in the first place. You must take your subjective beliefs into account. To make his point, Bayes used a metaphor of a table, upon which balls are rolled. The table is hidden from your view, and a white ball is rolled on it in such a way that its final position is entirely random: “There shall be the same probability that it rests upon any one equal part of the plane as another.” When the white ball comes to a rest, it is removed, and a line is drawn across the table where it was. You are not told where the line is. Then a number of red balls are also rolled onto the table. All you are told is how many of the balls lie to the left of the line, and how many to the right. You have to estimate where the line is … Richard Price (1723–1791) was another Nonconformist minister, who (as Bayes rightly guessed) was working at a chapel in Newington Green, North East London. At the time, Price was a much more well-known man than his older friend Bayes. He was well connected with radical thinkers: notably, he was friends with several of the Founding Fathers of the American Revolution. He exchanged letters with Thomas Jefferson55 and Benjamin Franklin, both of whom visited him in Newington Green, as did John Adams, the second president of the United States. Franklin in particular appears to have been a close friend. Price was also friends with the philosophers David Hume (of whom more later) and Adam Smith, and with William Pitt the Elder, the politician. Price is important to this story as the man who brought Bayes’s paper to wider attention: he showed the paper to the physicist John Canton in 1761, after Bayes’s death, and had it published in the Philosophical Transactions of the Royal Society two years later. Part of the reason it took so long for him to publish it was that Price didn’t just go over it for typos and misplaced commas; he was more than, in the words of the historian of statistics Stephen Stigler, “a loyal secretary.” Price had visions of his own for the work: while Bayes wrote the first half of the paper, the second half, containing all the possible practical applications of the theorem, was all Price. But what’s interesting is what motivated Price to do that. At the time, there was a divide among the Nonconformist ministries, between those who thought mathematics would lead to godlessness and those who thought it would help us understand God’s universe. Price was of the latter persuasion, and so, Stigler and Bellhouse believe, he wanted to use Bayes’ theorem to save God from David Hume. Hume, in his 1748 essay “Of Miracles,” argued that no amount of testimony should ever convince someone that a miracle, a violation of natural law, took place: he never actually said “extraordinary claims require extraordinary evidence,” but that’s the gist of it. “[No] testimony is sufficient to establish a miracle,” wrote Hume, “unless the testimony be of such a kind, that its falsehood would be more miraculous, than the fact, which it endeavours to establish.” If someone were to say that he had seen the dead restored to life, Hume continues, “I immediately consider with myself, whether it be more probable, that this person should either deceive or be deceived, or that the fact, which he relates, should really have happened.”62 This was pretty shocking stuff to a Christian nation, who firmly believed in at least one person coming back from the dead in the New Testament, and Hume’s essay was met with a hostile reaction. But the point is one of probability: we all have a lifetime’s experience of the laws of nature not being broken, and we also have a lifetime’s experience of people saying things that are not true. If someone says, “I saw a dead man come back to life,” most of us would consider it more likely that that someone is wrong, or lying, than that they actually saw a dead man come back to life. So, says Hume, we should ignore that testimony as irrelevant. But Price, newly armed with Bayes’ theorem, wanted to say that rare events do happen, and that even if you’ve seen the sun rise or the tide come in a million times, you can never be physically certain, in his phrase, that it’ll do so the next time … Price then goes on: Say you’re not talking about a die. Say you’re talking about watching the tide come in, twice every day. You’ve seen it a million times (you’re fourteen hundred years old). There is still a small, but real, possibility that on the million-and-first time, it just won’t. Rare events happen sometimes, and no amount of seeing them not happen will ever completely rule them out. Similarly—Price would say—you might have seen people fail to rise from the dead a large number of times, but you can’t ever say with certainty that it never happens. Hume saw Price’s work. In fact there was a rather lovely exchange between the two men, which I will tell you about just because it’s so nice to see two people who disagree so profoundly on something so important—God versus no God—behaving so civilly. Price included some mildly rude lines in his essay responding to “Of Miracles,” such as one suggesting that someone putting forward arguments such as Hume’s “would deserve more to be laughed at than argued with.” Then the two men met, and Hume, by all accounts a very affable and reasonable man, left Price both charmed and ashamed: in a second edition, he removed every disobliging comment (“it is indeed nothing but a poor though specious sophism” replaced with “I cannot hesitate in asserting it is founded on false principles,” for instance) and added a rather apologetic introduction saying that one shouldn’t accuse one’s opponent of bad faith or disingenuousness. And Hume, after Price’s apology, sent him a sweet letter saying that he had nothing to apologize for, that he was “a true Philosopher,” that he had treated Hume “with unusual Civility … as a man mistaken, but capable of Reason and conviction,” and that Price’s arguments were “new and plausible and ingenious.”
The person who developed Bayes’s insights into a mathematical method was Pierre-Simon Laplace, through an independent discovery. As McGrayne writes:
Browsing in the library’s stacks, [Laplace] discovered an old book on gambling probability, The Doctrine of Chances, by Abraham de Moivre. The book had appeared in three editions between 1718 and 1756, and Laplace may have read the 1756 version. Thomas Bayes had studied an earlier edition. Reading de Moivre, Laplace became more and more convinced that probability might help him deal with uncertainties in the solar system. Probability barely existed as a mathematical term, much less as a theory. To Laplace, the movements of celestial bodies seemed so complex that he could not hope for precise solutions. Probability would not give him absolute answers, but it might show him which data were more likely to be correct. He began thinking about a method for deducing the probable causes of divergent, error- filled observations in astronomy. He was feeling his way toward a broad general theory for moving mathematically from known events back to their most probable causes. Because humans can never know everything with certainty, probability is the mathematical expression of our ignorance: “We owe to the frailty of the human mind one of the most delicate and ingenious of mathematical theories, namely the science of chance or probabilities.” … [Laplace’s] “Mémoire on the Probability of the Causes Given Events” … provided the first version of what today we call Bayes’ rule, Bayesian probability, or Bayesian statistical inference. Not yet recognizable as the modern Bayes’ rule, it was a one-step process for moving backward, or inversely, from an effect to its most likely cause. As a mathematician in a gambling-addicted culture, Laplace knew how to work out the gambler’s future odds of an event knowing its cause (the dice). But he wanted to solve scientific problems, and in real life he did not always know the gambler’s odds and often had doubts about what numbers to put into his calculations. In a giant and intellectually nimble leap, he realized he could inject these uncertainties into his thinking by considering all possible causes and then choosing among them. Laplace did not state his idea as an equation. He intuited it as a principle and described it only in words: the probability of a cause (given an event) is proportional to the probability of the event (given its cause). Laplace did not translate his theory into algebra at this point, but modern readers might find it helpful to see what his statement would look like today:
where P( C | E) is the probability of a particular cause (given the data), and P( E | C) represents the probability of an event or datum (given that cause). The sign in the denominator represented with Newton’s sigma sign makes the total probability of all possible causes add up to one.
As Jason Rosenhouse describes the practical significance of Bayes’ theorem:
These insights were left largely unapplied in any sophisticated sense until they were rediscovered in the 1930’s and practically applied by an underwriter named Arthur Bailey. As McGrayne writes:
Arthur L. Bailey … was in charge of setting premium rates to cover riskd involving automobiles, aircraft, manufacturing, burglary, and theft for the American Mutual Alliance, a consortium of mutual insurance companies … Settling into his new job, Bailey was horrified to see “hard-shelled underwriters” using the semi-empirical, “sledge hammer” Bayesian techniques developed in 1918 for workers’ compensation insurance. University statisticians had long since virtually outlawed those methods, but as practical business people, actuaries refused to discard their prior knowledge and continued to modify their old data with new. Thus they based next year’s premiums on this year’s rates as refined and modified with new claims information. They did not ask what the new rates should be. Instead, they asked, “How much should the present rates be changed?” A Bayesian estimating how much ice cream someone would eat in the coming year, for example, would combine data about the individual’s recent ice cream consumption with other information, such as national dessert trends. As a modern statistical sophisticate, Bailey was scandalized. His professors, influenced by Ronald Fisher and Jerzy Neyman, had taught him that Bayesian priors were “more horrid than ‘spit,’” in the words of a particularly polite actuary3 Statisticians should have no prior opinions about their next experiments or observations and should employ only directly relevant observations while rejecting peripheral, nonstatistical information. No standard methods even existed for evaluating the credibility of prior knowledge (about previous rates, for example) or for correlating it with additional statistical information. Bailey spent his first year in New York trying to prove to himself that “all of the fancy actuarial [Bayesian] procedures of the casualty business were mathematically unsound.” After a year of intense mental struggle, however, he realized to his consternation that actuarial sledgehammering worked. He positively liked formulae that described “actual data. . . . I realized that the hard-shelled underwriters were recognizing certain facts of life neglected by the statistical theorists.” He wanted to give more weight to a large volume of data than to the frequentists’ small sample; doing so felt surprisingly “logical and reasonable.” Bailey began writing an article summarizing his tumultuous change in attitude toward Bayes’ rule. Bailey worked out mathematical methods for melding every scrap of available information into the initial body of data. He particularly tried to understand how to assign partial weights to supplementary evidence according to its credibility, that is, its subjective believability. His mathematical techniques would help actuaries systematically and consistently integrate thousands of old and new rates for different kinds of employers, activities, and locales. By 1950 Bailey was a vice president of the Kemper Insurance Group in Chicago and a frequent after-dinner speaker at black-tie banquets of the Casualty Actuarial Society. He read his most famous paper on May 22, 1950. Its title explained a lot: “Credibility Procedures: Laplace’s Generalization of Bayes’ Rule and the Combination of Collateral [that is, prior] Knowledge with Observed Data.” The year of Bailey’s death, one of his admirers was sipping a martini at the Insurance Company of North America’s Christmas party when INA’s chief executive officer, dressed as Santa Claus, asked an unthinkable question: Could anyone predict the probability of two planes colliding in midair? Santa was asking his chief actuary, L. H. Longley-Cook, to make a prediction based on no experience at all. There had never been a serious midair collision of commercial planes. Without any past experience or repetitive experimentation, any orthodox statistician had to answer Santa’s question with a resounding no. But the very British Longley-Cook stalled for time. “I really don’t like these things mixed with martinis,” he drawled. Nevertheless, the question gnawed at him. Within a year more Americans would be traveling by air than by railroad. Meanwhile, some statisticians were wondering if they could avoid using the ever-controversial subjective priors by making predictions based on no prior information at all. Longley-Cook spent the holidays mulling over the problem, and on January 6, 1955, he sent the CEO a prescient warning. Despite the industry’s safety record, the available data on airline accidents in general made him expect “anything from 0 to 4 air carrier-to-air carrier collisions over the next ten years.” In short, the company should prepare for a costly catastrophe by raising premium rates for air carriers and purchasing reinsurance. Two years later his prediction proved correct. A DC-7 and a Constellation collided over the Grand Canyon, killing 128 people in what was then commercial aviation’s worst accident. Four years after that, a DC-8 jet and a Constellation collided over New York City, killing 133 people in the planes and in the apartments below … News of [Arthur Bailey’s] achievement percolated slowly and haphazardly to university theorists.
In the next essay in this series, we’ll see how figuring out whether James Madison wrote certain essays led to ChatGPT.

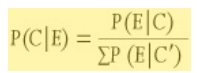

Paul, This is really a marvelous series developing. Enjoying each episode. And learning history I never knew. You are wasted on politics...Many thanks.